Doorsneden

Definitie | Drievlakspunt | Voorbeelden ][  Drievlaksstelling | Stellingen | Overzicht stereo

Opmerking vooraf
Onder het construeren van lijnen, punten, vlakken e.d. in de ruimtemeetkunde verstaan we in eerste instantie het beschrijven (in woorden dus) van de uit te voeren handelingen.
De daadwerkelijke constructie kan op basis daarvan in een 2-dimensionale projectiefiguur indien gewenst worden uitgevoerd.
[einde Opmerking]

Definitie terug
De doorsnede van een plat vlak met een ruimtelijk lichaam is de meetkundige plaats van de punten die én in het platte vlak én op het ruimtelijk lichaam gelegen zijn.

Opmerking. In voorkomende gevallen wordt onder doorsnede ook begrepen het snijpunt van een lijn en een vlak en ook wel de snijlijn van twee vlakken.

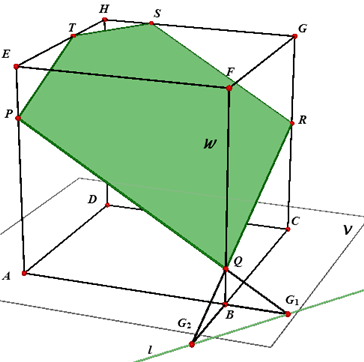
Voorbeeld. In onderstaande figuren is de doorsnede getekend van het vlak W = PQRST met de kubus ABCD.EFGH.

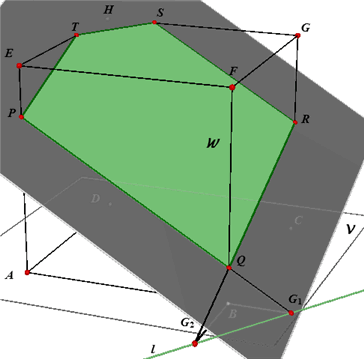doorsnede1     doorsnede2

De punten G1 en G2 zijn de snijpunten van het grondvlak V en de lijnen PQ en QR. De lijn l = G1G2 ligt dus eveneens in V en in W; l is daarmee de snijlijn van de vlakken V en W.
De lijn l wordt wel de grondlijn van de doorsnede PQRST genoemd.

Drievlakspunt terug
Bij de constructie van de doorsnede van een vlak met een ruimtelijk lichaam kan de grondlijn een belangrijke rol spelen.
Bekijken we het punt G1 in bovenstaande figuren, dan kunnen we vaststellen dat G1 gelegen is in de vlakken V, W én in het zijvlak ABFE van de kubus.
Het punt G1 is daarmee het zogenoemde drievlakspunt van V, W en ABFE (zie Drievlaksstelling); G1 is het snijpunt van de drie snijlijnen van deze vlakken (te weten: l, AB en PQ).
Evenzo is het punt G2 het drievlakspunt van de vlakken V, W en BCGF.
Nb. Op de lijn l liggen ook nog andere drievlakspunten.

Voorbeelden terug
Voorbeeld 1
¤ Construeer de doorsnede van de piramide X.ABCDE met het vlak PQR = W waarbij P op XA, Q op XB en R op XC ligt.

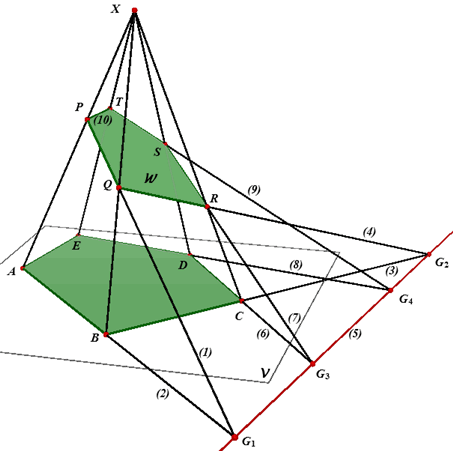doorsnede3 We maken bij deze constructie gebruik van de grondlijn die de snijlijn is van het vlak W met het vlak V = ABCDE.

De lijnen PQ (1) en AB (2) liggen in het zijvlak XAB. Hun snijpunt G1 ligt op de grondlijn.
G1 is dus het drievlakspunt van V, W en XAB.

Nb. De tussen haakjes geplaatste getallen geven de volgorde aan van de constructie van de lijnen.

De lijnen BC (3) en QR (4) liggen in het zijvlak XBC. Hun snijpunt G2 ligt dus eveneens op de grondlijn.
De grondlijn (5) kan nu worden getekend.

De snijlijn van W en het vlak XCD gaat door het punt R en ligt dus in het vlak XCD.
Het drievlakspunt G3 van die vlakken met V is dan het snijpunt van CD (6) met de grondlijn.
De lijn G3R (7) snijdt de ribbe XD dan in het punt S.

De snijlijn van W met het vlak XDE gaar door het punt S en ligt dus in het vlak XDE.
Het drievlakspunt G4 van die vlakken met V is dan het snijpunt van DE (8) met de grondlijn.
De lijn G4S (9) snijdt de ribbe XE dan in het punt T.

De snijlijn van W met het zijvlak XAE is dan de lijn PT (10).
Daarmee is vijfhoek PQRST de doorsnede van W met de piramide.

Voorbeeld 2
Het is bij een constructie van een doorsnede niet noodzakelijk gebruik te maken van een grondlijn.
In de onderstaande figuur is voor de constructie van de doorsnede van de piramide X.ABCD met het vlak W = PQR (opvolgend op XA, XB en XC) gebruik gemaakt van de zogenoemde diagonaalvlakken van de piramide.

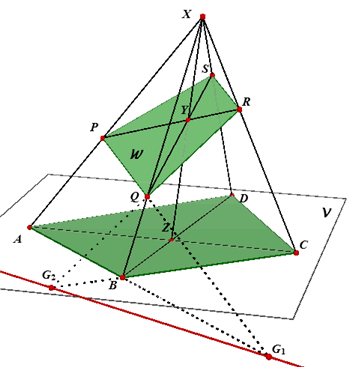doorsnede4 De doorsnede van het vlak W met het diagonaalvlak XAC is de lijn PR.
De doorsnede van de beide diagonaalvlakken XAC en XBD is de lijn XZ (waaarbij Z het snijpunt is, gelegen in V, van de lijnen AC en BD).
Het punt Y (het snijpunt van PR en XZ is dus het drievlakspunt van de diagonaalvlakken en het vlak W.
De snijlijn van W met XBD gaat dus door Y en door Q. Deze lijn snijdt de ribbe XD dan in het punt S.
De doorsnede van de piramide met vlak W is dus de vierhoek PQRS.

Opmerking 1
In de figuur is de snijlijn van de vlakken V en W (de grondlijn) eveneens opgenomen (met daarop de punten G1 = AB & PQ en G2 = BC & QR).
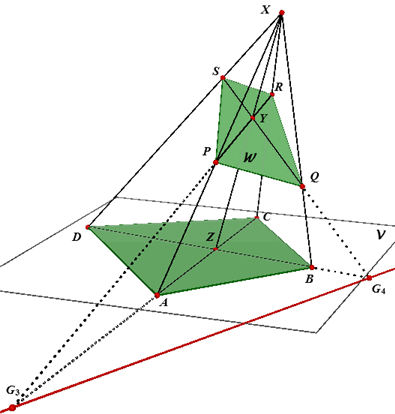doorsnede5 Opmerking 2
Uiteraard liggen ook de snijpunten van PR en AC (G3) en van QS en BD (G4) op de grondlijn.

G3 is het drievlakspunt van V, W en XAC.
G4 is het drievlakspunt van V, W en XBD.

Voorbeeld 3
¤ Knot het prisma ABCD.EFGH af met een vlak W door P (op DH en Q (op BF) dat evenwijdig is met de lijn AC.

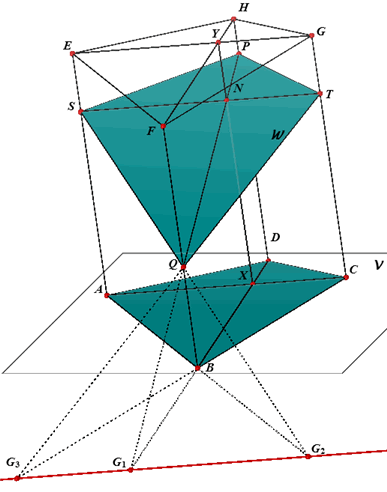doorsnede6 Eerste methode
De lijn PQ en de lijn BD snijden elkaar op de grondlijn in het punt G1.
Het vlak W gaat door G1 en is evenwijdig met de lijn AC. De grondlijn is hier dus een lijn die evenwijdig is met AC.
Op basis daarvan kan de grondlijn worden geconstrueerd (door G1 en // AC).

G2 is het drievlakspunt van W, V en ABFE. De lijn G2Q nijdt de ribbe AE in het punt S.

G3 is het drievlakspunt van V, W en BCGF. De lijn G3Q snijdt de ribbe CG in het punt T.

Hiermee is PSQT het bovenvlak van het afgeknotte prisma.

Tweede methode
De diagonaalvlakken ACGE en BDHF snijden elkaar volgens de lijn XY (X in V en Y in EFGH).
Het punt N = PQ & XY is het drievlakspunt van die diagonaalvlakken en het vlak W.
De lijn door N evenwijdig met AC snijdt dan de ribben AE en CG in de punten S en T.

Opmerking. De ene methode kan dienen als controle van de juiste constructie bij de andere methode.

begin pagina
[p: doorsneden.htm] laatste wijziging op 08-10-2008 (08-10-2008)