Stelling van Van Schooten (1646)

Overzicht ][ Meetkunde | Geschiedenis | Cabri

Overzicht

Stelling van Van Schooten
Drie bewijzen
     2.1. Min of meer direct
     2.2. Via de stelling van Ptolemaeus
     2.3. Via de cosinusregel
Een er mee samenhangende ongelijkheid
Historie
Referenties
Download

1. Stelling van Van Schooten

Stelling 1a
Voor een punt P op de omcirkel van een gelijkzijdige driehoek ABC geldt: als AP het lijnstuk BC snijdt, dan is AP = BP + CP.
(Frans van Schooten jr., ca. 1615-1660, Nederland; zie ook Referenties [c])

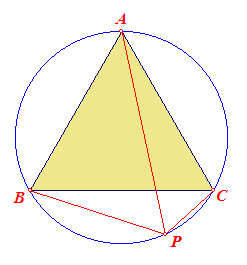of anders geformuleerd:

Stelling 1b
Voor een punt P op de omcirkel van een gelijkzijdige driehoek geldt dat het langste verbindingslijnstuk van P met een hoekpunt gelijk is aan de som van de beide andere verbindingslijnstukken.

Zie verder ook de paragraaf Historie.

Klik hier >< voor een CabriJavapplet bij deze stelling.

We geven van de stelling allereerst drie (moderne) bewijzen >>>.
In de paragraaf Historie staat het bewijs van Van Schooten zelf.

2. Drie bewijzen

2.1. Min of meer direct

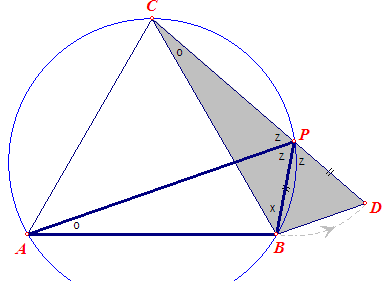Op het verlengde van CP kiezen we het punt D zo, dat PD = PB.
Nu zijn de driehoeken ABP en CBD congruent (ZHH of ZHZ), immers driehoek BDP is een gelijkzijdige driehoek.
En daaruit volgt:

AP = CD = PD + PC = PB + PC

Opmerking. In de figuren duidt de letter 'z' op een hoek van 60°.

2.2. Via de stelling van Ptolemaeus

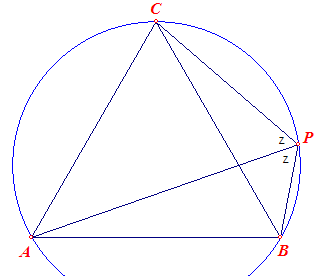Vierhoek ABPC is een koordenvierhoek.
In deze koordenvierhoek geldt volgens de stelling van Ptolemaeus:

AP · BC = AB · PC + BP · CA

Met AB = BC = CA = l volgt dan:
AP · l = l · PC + BP · l
of
AP = PC + BP

2.3. Via de cosinusregel

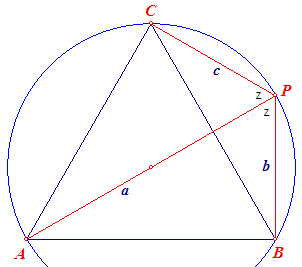In bovenstaande figuur stellen we verder PA = a, PB = b en PC = c.
Toepassing van de cosinusregel geeft dan
in driehoek APC: l² = a² + c² - 2ac cos 60° = a² + c² - ac ......(1)
in driehoek ABP: l² = a² + b² - 2ab cos 60° = a² + b² - ab ......(2)
Aftrekking van (1) en (2) levert:
b² - c² = a(b - c)
zodat na deling door b - c (met b ongelijk aan c) overblijft:
a = b + c

Voor b = c zie nevenstaande figuur.
Nu zijn de driehoeken ABP en ACP rechthoekig in opvolgend B en C. Beide driehoeken zijn dan 30-60-90-driehoeken, zodat dan
a = 2b = 2c = b + c

Zie verder eventueel de paragraaf Historie >>>.

3. Een er mee samenhangende ongelijkheid

Stelling 2
Voor een punt P geldt bij een gelijkzijdige driehoek ABC steeds PA + PB ³ PC.

Bewijs:

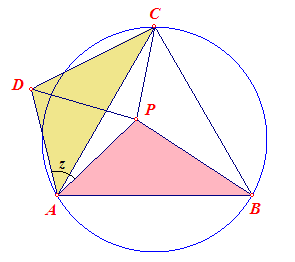Teken de gelijkzijdige driehoek APD waarvan hoek PAD dezelfde orientatie heeft als hoek BAC (via rotatie van PA om A over 60°).

We hebben nu, afhankelijk van de overlap van de hoeken:
BAP = BAC - PAC = PAD - PAC = DAC
of
BAP = BAC + PAC = PAD + PAC = DAC
Ook is AB = AC en AP = AD, zodat de driehoeken ABP en ACD congruent zijn (ZHZ).
Dus: BP = CD.
De driehoeksongelijkheid (in driehoek PCD) geeft dan:

PC £ CD + DP = PB + PA

Opmerking
We kunnen dus met de lijnstukken PA, PB, PC als zijden een driehoek construeren. Een dergelijke driehoek wordt in dit verband wel Pompeiu-driehoek genoemd (naar Dimitrie Pompeiu, 1873-1954, Roemenië).
Als P op de omcirkel van ABC ligt, is de Pompeiu-driehoek ontaard (lijnstukken vallen samen).

Klik hier >< voor een CabriJavapplet bij stelling 2.

4. Historie
¤ Met dank aan Jan van Maanen (FIsme, Utecht)) voor de scans, feiten, ... (in persoonlijke correspondentie; januari 2006).

Van Schooten vermeldt de stelling in zijn
"De organica conicarum sectionum in plano descriptione, Tractatus" (Leiden: Ex Officina Elzeviriorum, 1646; klik hier voor de titelpagina)
en wel in een appendix ervan: "Appendix, de cubicarum aequationum resolutione" (pp. 91-117)
De naar Van Schooten (mogelijk door Newton) vernoemde stelling is daarin de eerste stelling (p. 92):

Stelling van Van Schooten
				Theorema I. Si fuerit triangulum aequilaterum MNL cir- culo inscriptum, atque ex L educta utcunque recta LF usque ad circumferentiam in F, quae secet MN in O, junctaeque rectae MF, FN: Dico FL aequalem esse ipsis MF, FN simul sumptis.

Vertaling [dk]
Als er een gelijkzijdige driehoek MNL [gegeven] is, ingeschreven in een cirkel, en ook uit L willekeurig een lijn LF is getrokken tot aan de cirkelomtrek in F, die MN snijdt in O, en toegevoegd de lijnen MF, FN: [dan] beweer ik dat FL gelijk is aan deze MF, FN samengenomen.

De appendix over 'kubische vergelijkingen' komt ook voor in Van Schootens Latijnse vertaling (Geometria, eerste editie 1649) van La Géométrie van René Descartes (in ieder geval in de editie van 1659, deel 1, pp. 345-368), en wel op pag. 346, in dezelfde bewoordingen.

Bewijs (Appendix de cubicarum aequationum resolutione, p. 92-93 / in vertaling van en met toelichting van Jan van Maanen):

De driehoeken LNO en LNF zijn namelijk gelijkvormig, want ze hebben hoek L gemeen, en hoek LNO, ofwel^[1] LMN gelijk aan hoek LFN wegens Elementen III, 21^[2] en daarom is ook het derde paar hoeken LON en NFL gelijk, wegens I, 32^[3]. En daarom^[4] wegens VI, 4 geldt dat NO staat tot LN als FN tot LF. En net zo volgt uit de gelijkvormigheid van de driehoeken LMO en LFM dat MO staat tot LM als FM tot LF. En dus, wegens V, 24^[5,6] zal gelden: zoals NO en MO bijeengenomen staan tot LN, zo staan FN en FM bijeengenomen tot LF. Maar NO en MO zijn samen LN; en daarom zullen ook FN en FM samen LF zijn. Hetgeen te bewijzen was.

Toelichting
[1] Wegens de gelijkzijdigheid.
[2] Elem. III, 21 zegt dat omtrekshoeken die op dezelfde boog staan, gelijk zijn. In de redactie van Dijksterhuis: "In een cirkel zijn de hoeken in hetzelfde segment aan elkaar gelijk."
[3] Elem. I, 32 zegt dat de drie hoeken van een driehoek gelijk zijn aan twee rechte hoeken.
[4] D.w.z. uit de gelijkvormigheid volgt ...
Elem. VI, 4 zegt (vertaling Dijksterhuis): In gelijkhoekige driehoeken zijn evenredig de zijden om de gelijke hoeken en homoloog die zich onder de gelijke hoeken spannen.
[5] Elem. V, 24 zegt (in moderne terminologie): als a : c = d : f en b : c = e : f, dan (a + b) : c = (d + e) : f (en zo staat het ook bij Heath).
[6] En niet alleen wegens Elem. V, 24 maar ook omdat bovendien LM = LN, wegens de gelijkzijdigheid.

5. Referenties

[a]		Euclides: Elementen (zie het overzicht op deze website)
[b]		D. Pompeiu: Opera mathematicâ. Boekarest: Ed. Academiei (1959).
[c]		Jeanine Daems: Frans van Schooten jr. (op www.wiskonst.nl)
[d]		Jan van Maanen: Frans van Schooten jr. In: Pythagoras (juni 1997); via Kennislink Jan van Maanen: Descartes en zijn Nederlandse profeten. In Pythagoras (februari 1998); via Kennislink
[e]		József Sándor: On the Geometry of Equilateral Triangles. Forum Geometricorum Vol. 5 (2005), pp. 107-117 (PDF-bestand, FG200514)
[f]		www.fransvanschooten.nl ("Mathematische Oeffeningen" door Henk Hietbrink)

6. Download
De bij de applets gebruikte Cabri-figuren kunnen in een bestand worden gedownload via deze website.
Klik hier om het downloadproces te starten (ZIP-bestand, ca. 4 kB).

[p : vanschooten.htm] laatste wijziging op: 25-06-2008