De oppervlakte van een cirkel

Cirkelfunctie | Oppervlakte en pi | Integratie | Referenties  ][ Analyse | Maple

3.141592653589793238462643383279502884197169399375105820974944...

Zie ook de pagina "Pi volgens Archimedes"
Zie ook de pagina "Berekening van Pi"
Zie ook de pagina "Benaderingen van Pi"

Op deze pagina wordt gebruik gemaakt van enkele notaties uit Maple V, Release 4.

1. Cirkelfunctie

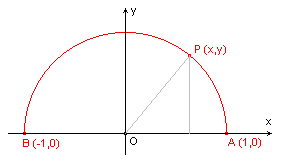figuur 1  pi1 We bekijken de functie
   f(x) = Ö(1 - x 2)    voor x in [-1 ; 1].
De grafiek van deze functie (zie figuur 1) is een halve cirkel met middelpunt  O en straal 1, immers met y=Ö(1 - x 2) vinden we x2 + y2 = 1, zodat voor ieder punt P(x, y) van de grafiek van f geldt: OP = 1 (volgens de stelling van Pythagoras).

2. Oppervlakte en p
We kunnen nu de oppervlakte van de kwartcirkel met x in [0 ; 1] (via een serie Maple-opdrachten) direct schrijven als 

> f:= x-> sqrt(1-x^2);
f:=x->Ö(1-x2)
> kwartO := Int(f(x), x=0..1);

kwartO:=imagespi3

Deze integraal (een Riemann-integraal) berust op onderstaande grafische interpretatie van een benadering van de oppervlakte via een Riemann-som van de oppervlaktes van een aantal rechthoeken.
In figuur 2 hebben we 8 (benaderende) rechthoeken getekend met behulp van de Maple-opdracht

> leftbox(f(x), x=0..1, 8);
figuur 2  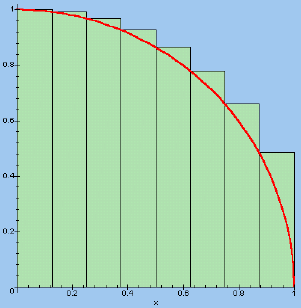imagespi2

We krijgen dan een benadering van de oppervlakte van de kwartcirkel via

> S8:=leftsum(f(x), x=0..1, 8);

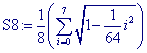
imagespi4

Zodat we in dit geval als benadering van p krijgen:

> 4*evalf(S8);
3.339819144

De benadering van de oppervlakte onder de grafiek van f (dus van p) wordt beter, als we meer rechthoeken gebruiken.
We zetten de aantallen te gebruiken rechthoeken eerst in een rij:

> boxes:=[ seq (i^2, i=2..14) ];
boxes := [4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196]

Voor elk getal in deze rij berekenen we nu de linkersom: met

> seq ( evalf(4*leftsum(f(x), x=0..1, n)), n=boxes );
3.495709068, 3.320407605, 3.248253038, 3.212196310, 3.191708477,
3.178982603, 3.170546913, 3.164671478, 3.160417032, 3.157238270,
3.154801142, 3.152891803, 3.151368237

De waarde van p vinden we dan door oneindig veel rechthoeken te kiezen:

> 4 * Limit (leftsum(f(x), x=0..1, n), n=infinity);

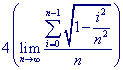
imagespi5

Een andere schrijfwijze voor deze Riemann-som is

> pi := 4* Int(f(x), x=0..1);

imagespi6

De waarde van p vinden we dan met

> evalf(pi);
3.141592654

3. Integratie
We kunnen de integraal pi3 ook op een "schoolse manier" berekenen.
We laten twee methodes zien:
     3.1. Substitutiemethode
     3.2. Partiële integratie

3.1 Substitutiemethode
We substitueren x = sin(t) in de integraal I = pi3.
We krijgen dan:
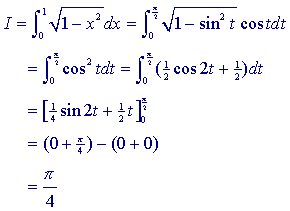
   pi2-31

3.2. Partiële integratie
   imagespi31
Vervolgens vinden we dan (partieel):
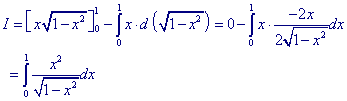
   imagespi32
We schrijven nu x2 (in de teller) als 1 - (1 - x2), zodat
   imagespi33
Daaruit vinden we dan
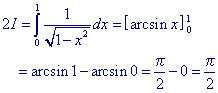
   imagespi35
Zodat    imagespi34

4. Referenties
In de literatuur en op het web is natuurlijk meer informatie over p te vinden, zeker omdat p de "Mount Everest of Mathematics" (Dr. Roger Webster, University of Sheffield, Engeland) kan worden genoemd.
Hieronder slechts een selectie.

[1]  Carothers, Neil, A Common Book of Pi (BGSU. Bowling Green, Ohio - USA)
[2] Dörrie, H., 100 Great Problems of Elementaty Mathematics, pg.184-188, Dover Publcations, New York, 1965
[3] Finch, S., Archimedes' Constant (MathSoft Inc., USA)
[4] Heath, Sir Thomas, A History of Greek Mathematics, vol. II, pg. 50-56, Dover Publications, New York, 1981
[5] Ravenstein, W. van, De geschiedenis van Pi (NL)
[6] Tijdschrift Pythagoras, p - Links naar dit magische getal (NL; een verzameling links naar andere sites)
[7] Weisstein, Eric, W., Archimedes Algorithm (CRC Concise Encyclopedia, USA)

up

[pi2.htm] laatste wijziging op: 23-02-2001