Isodynamische punten

Overzicht  ][  Apollonius-cirkels | Meetkunde

Overzicht terug

  1. Inleiding cabrisignal
  2. Lemoine-punt en Lemoine-lijn cabrisignal
  3. Perspectiviteiten
  4. Een gelijkzijdige driehoek
  1. Download

1. Inleiding terug
Op de pagina "Cirkels van Apollonius" is oa. bewezen:

Stelling 1
De drie Apollonius-cirkels van een ongelijkzijdige driehoek snijden elkaar in twee punten.
.
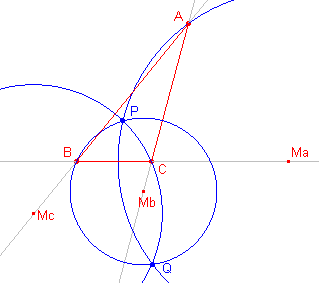apol21 De gemeenschappelijke punten P en Q heten isodynamische punten.

Een verklaring van de naam is wellicht op z'n plaats.
Grieks: isoV = gelijk, dunamiV = macht.
De beide punten (P en Q) hebben gelijke machten tov. de driehoek.
De macht van een punt X tov. hoekpunt A van een hoekpunt van driehoek ABC wordt gedefinieerd door
m(X, A, ABC) = XA · BC

In het bewijs van de stelling zien we dat voor het punt P geldt:
PA / PB = b /a = AC / BC, zodat
PA · BC = PB · AC, en dus
m(P, A, ABC) = m(P, B, ABC)

Gevolg
De C-Apollonius-cirkel is de meetkundige plaats van de punten P met gelijke machten tov. de hoekpunten A en B van ABC.
De punten P en Q hebben dus gelijke machten tov. elk van de hoekpunten van driehoek ABC. ¨

Klik hier >Animatie< voor een CabriJavapplet mbt. de Apollonius-cirkel als meetkundige plaats.

2. Lemoine-punt en Lemoine-lijn terug

Op de pagina "Cirkels van Apollonius" is ook bewezen:

Stelling 2
[1]
De drie middelpunten van de Apollonius-cirkels van een driehoek zijn collineair.
Deze collineatie-as heet Lemoine-lijn.
[2]
De Apollonius-cirkels van een driehoek snijden de omgeschreven cirkel van die driehoek loodrecht.

We bewijzen nu:

Stelling 3
Het Lemoine-punt K is de pool van de Lemoine-lijn ten opzichte van de omcirkel.

Opmerking
Hiermee is de naamgeving van de Lemoine-lijn verklaard: de lijn is de poollijn van het Lemoine-punt tov. de omcirkel.
[einde Opmerking]

Klik hier >Animatie< voor een CabriJavapplet ter illustratie van Stelling 2.1 en Stelling 3.

Bewijs:

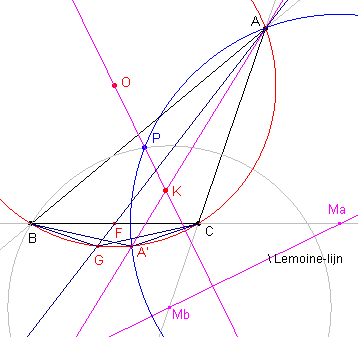apol22 Zij A' het van A verschillend snijpunt van de omcirkel en de A-Apollonius-cirkel.
Nu is AA' de poollijn van Ma tov. de omcirkel (zie Stelling 2.2).
De pool van MaMb (de Lemoine-lijn) moet dus liggen AA'.
We zullen nu aantonen, dat AA' een symmediaan is van ABC.

Uit A' op cirkel Ma volgt A'B · AC = A'C · AB (machten tov de driehoek; Gevolg van Stelling 1).
Zodat
A'B : A'C = b : c ......(1)
Zij nu F het midden vab BC, en G het van A verschillend snijpunt van de omcirkel met AF.
In de koordenvierhoek ABGC geldt dan:
(AB · BG) : (AC · CG) = BF : FC ......(2)
Uit (2) volgt dan eenvoudig: BG : CG = b : c ......(3)
(1) en (3) geven dan (vanwege de gemeenschappelijke koorde BC): BGC @ CA'B, zodat
CG = BA'
waaruit blijkt dat CAG = BAA'.
En inderdaad, AA' is dan symmediaan van driehoek ABC.

Evenzo zijn er punten B' en C' waarbij BB' en CC' symmedianen zijn; dit zijn de poollijnen van Mb en Mc tov. de omcirkel
Het snijpunt K van deze symmedianen is dus de pool van de lijn MaMbMc tov. de omcirkel. ¨

Eenvoudig volgt nu ook

Stelling 4
De isodynamische punten worden harmonisch gescheiden door O en K, waarbij O, K, P en Q collineair zijn, met OK _|_ Lemoine-lijn.

Bewijs:
De omcirkel snijdt de Apollonius-cirkels loodrecht. Hieruit volgt, dat O op PQ ligt en dat tevens PQ _|_ Lemoine-lijn.
K is de pool van MaMbMc tov. de omcirkel, zodat K moet liggen op de loodlijn uit O op die rechte; dwz. K ligt op PQ.
Tenslotte: AA' is de poollijn van O tov cirkel Ma. waaruit volgt dat (OKPQ) = -1. ¨

Opmerking
¤ Zie verder ook de pagina "Harmonikaal"
[einde Opmerking]

3. Perspectiviteiten terug

We hebben op de pagina "Pool en poollijn tov. een cirkel" de stelling  (daar stelling 4):

Hulpstelling
Is ABCD een volledige vierhoek beschreven in een cirkel, dan is elk diagonaalpunt van de vierhoek de pool van de lijn bepaald door de beide andere diagonaalpunten.

Deze stelling gebruiken we in het bewijs van de volgende

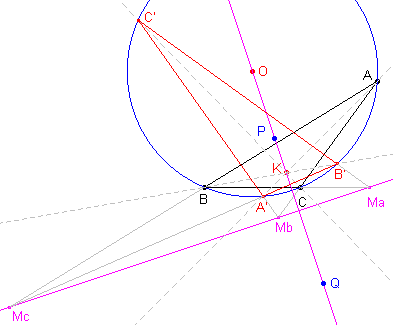apol24
Stelling 5
A'BC' is de driehoek met als hoekpunten de snijpunten van de symmedianen van ABC met de omcirkel.
De driehoeken ABC en A'B'C'  zijn perspectief in K met de Lemoine-lijn als perspectief-as.

Bewijs:
De driehoeken zijn perspectief in A (vanwege de constructie).
In de volledige vierhoek ABA'B' zijn Ken en het snijpunt (noem het even S) van AB en A'B' diagonaalpunten.
S ligt dus op de poollijn van K (zie Hulpstelling). Met andere woorden: A'B' gaat door Mc.
Evenzo gaat B'C' door Ma en C'A' door Mb.
De Lemoine-lijn is dus perspectief-as van beide driehoeken. ¨

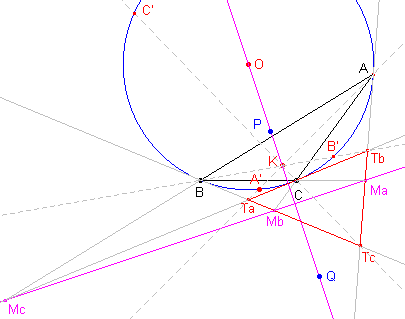apol25
Stelling 6
Driehoek ABC en diens raaklijndriehoek TaTbTc zijn perspectief in K met de Lemoine-lijn als perspectief-as.

Bewijs:
Volgens Stelling 2.2 gaat de raaklijn in A door Ma (enz.). De beide driehoeken hebben dus MaMbMc als perspectief -as.
AA' is de poollijn van Ma tov. de omcirkel. AA' gaat dus door de pool van Ta van BC tov. de omcirkel. ATa gaat dus door K.
En evenzo gaan BTa en CTa door K.
K is dus centrum van de perspectiviteit. ¨

4. Een gelijkzijdige driehoek terug

Stelling 7
De voetpuntsdriehoek van een isodynamisch punt is gelijkzijdig.

Bewijs:

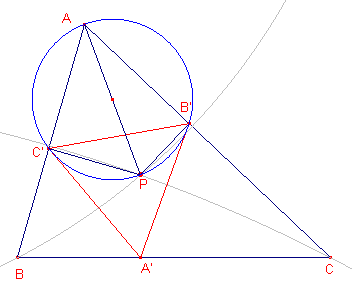apol26 Zij P een punt in het vlak van driehoek ABC en A'B'C' de voetpuntsdriehoek van P.
We onderstellen, dat A'B'C' gelijkzijdig is.
Nu is in driehoek AB'C' volgens de sinusregel:
B'C'/sin(A) = 2r (waarbij r de straal is van de omcirkel van AB'C').
Omdat AC'PB' een koordenvierhoek is, hebben we AP = 2r, zodat
B'C' = AP sin(A)
Evenzo: A'C' = BP sin(B)
Uit A'C' = B'C' volgt dan:
AP : BP = sin(B) : sin(A) = b : a.
Het punt P ligt dus op de C-Apollonius-cirkel van driehoek ABC (definitie van Apollonius-cirkel).
En analoog hebben we (bijvoorbeeld) P op de A-Apollonius-cirkel van ABC.
P is dus één van de isodynamische punten van driehoek ABC. ¨

Opmerkingen
[1]
Zie voor een ander bewijs van Stelling 7, in samenhang met inversie, de pagina "Inversie".
[2]
Zie op de pagina "Inversie" ook het bewijs van de

Stelling 8
De isodynamische punten van een driehoek zijn elkaars inversen bij een inversie ten opzichte van de omgeschreven cirkel van die driehoek.

[einde Opmerkingen]

5. Download terug
De figuren die gebruikt zijn in de CabriJavapplets op deze pagina, kunnen in één bestand via deze website worden gedownload.
In het bestand zijn ook de applet-figuren opgenomen van de pagina "Apollonius-cirkels".
Klik hier om het downloadproces te starten (ZIP-bestand; ca. 5kB)

begin pagina
[apolcirk2.htm] laatste wijziging op: 22-10-02