Hyperbolische meetkunde [1]: het Poincaré-model

Pagina-overzicht ][ Complexe afbeeldingen | Meetkunde

Begin

0. Overzicht
Deze pagina is een vervolg op de pagina's over Afbeeldingen in het complexe vlak.
De hyperbolische meetkunde wordt op deze pagina geïntroduceerd als een toepassing van Möbius-transformaties op een deelverzameling van het Euclidische vlak.

Euclidische meetkunde
     Definities
     Hulpstelling 1
     Hulpstelling 2
Hyperbolische meetkunde, het Poincaré-model, een inleiding
Definities (afspraken)
Animatie
Twee stellingen (hyperbolisch)

1. Euclidische meetkunde
Voorafgaande aan de introductie van de zogenoemde hyperbolische meetkunde bewijzen we allereerst enkele stellingen uit de (gewone) Euclidische meetkunde. Deze stellingen kunnen van dienst zijn bij constructies en bewijzen in het te behandelen model van de hyperbolische meetkunde.
Allereerst een tweetal definities.

Definities (Euclidisch)
[1] Onder de hoek tussen een rechte lijn en een kromme lijn in een punt (een snijpunt van beide) verstaan we de hoek tussen die rechte lijn en de raaklijn in dat punt.
[2] Onder de hoek tussen twee kromme lijnen in een punt (een snijpunt van beide) verstaan we de hoek tussen de raaklijnen in dat punt aan de beide kromme lijnen

Zie het Cabri-werkblad "Loodrecht snijden".
Op dit werkblad staat ook de definitie van de hoek tussen twee snijdende rechte lijnen.

Op het genoemde werkblad wordt onder meer de volgende stelling bewezen:

figuur 1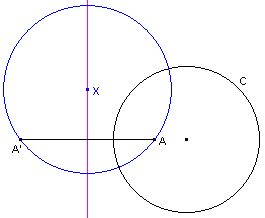

Hulpstelling 1 (Euclidisch)
De verzameling van de middelpunten van cirkels die door een punt A gaan en een gegeven cirkel C loodrecht snijden, is de middelloodlijn van het lijnstuk AA', waarbij A' het beeld is van A bij de inversie ten opzichte van de cirkel C (zie figuur 1).

Bewijs: zie dus het Cabri-werkblad "Loodrecht snijden".

Op basis van deze stelling bewijzen we:

Hulpstelling 2 (Euclidisch)
Door een punt A op een lijn m gaan 0, 1 of oneindig veel cirkels die een gegeven cirkel C loodrecht snijden.

Bewijs: (zie figuur 2)

figuur 2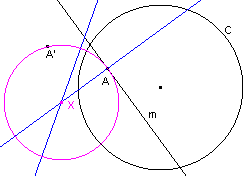

De meetkundige plaats van de middelpunten van cirkels die de lijn m in A raken is de loodlijn x₁ in A op m.
De meetkundige plaats van de middelpunten van cirkels door A die loodrecht staan op de cirkel C is de middelloodlijn x₂van het lijnstuk AA' (waarbij A' het beeld is van A bij inversie tov. de cirkel (zie Hulpstelling 1).
Het snijpunt van x₁ en x₂ is het middelpunt van de gezochte cirkel.
In het algemeen hebben de lijnen x₁ en x₂ één snijpunt. In het algmeen is er dus 1 cirkel.

.Als de lijnen x₁ en x₂ evenwijdig zijn er geen cirkels die de gevraagd eigenschappen hebben (zie figuur 3a).
De lijn m gaat in dit geval door het middelpunt van de cirkel C, waarbij A niet op de cirkel ligt.
Ook als A op de cirkel ligt en de lijn m niet door het middelpunt van de cirkel gaat, zijn er geen oplossingen (x₂ bestaat dan niet).
Als de lijnen x₁ en x₂ samenvallen zijn er oneindige veel cirkels die de gevraagde eigenschappen hebben; in dit geval voldoet namelijk elk punt op de lijn x₁ als middelpunt (zie figuur 3b).
Dit is het geval als A op de cirkel ligt, terwijl m door het middelpunt van de cirkel gaat. ¨

figuur 3a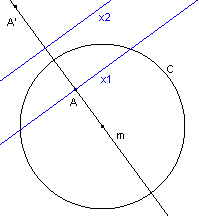

figuur 3b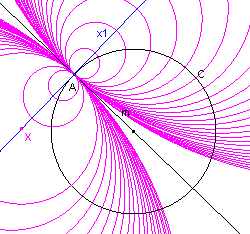

Opmerking
Cirkels die elkaar loodrecht snijden, worden ook wel orthogonaal cirkels genoemd.
[einde Opmerking]

2. Hyperbolische meetkunde, het Poincaré-model, een inleiding
In het Euclidische vlak kiezen we een cirkel C met middelpunt O die door een punt E gaat.
We normeren daarbij zo, dat OE = 1.
De (Euclidische) lijn door O en E noemen we zoals gebruikelijk x-as; de lijn door O loodrecht op de x-as noemen we y-as.
Hierdoor is dus op de gebruikelijke wijze een rechthoekig coördinatenstelsel in het Euclidische vlak vastgelegd.

We beschouwen nu in het bijzonder de punten van de cirkel en de punten van het vlakdeel dat binnen de cirkel gelegen is.
Daarnaast staan we (voorlopig althans) alleen die Möbius-transformaties toe, die de cirkel (niet-puntsgewijs) op zichzelf afbeelden en daarbij ook het binnengebied van de cirkel op zichzelf.
Deze verzameling van M-transformaties (die dus de cirkel en het binnengebied afbeelden op zichzelf) geven we ook wel aan met H.
Deze transformaties werden onderzocht op de pagina "Complex[3]".

Definities (naamgeving)

horizon	:	de cirkel
disk	:	het binnengebied van de horizon (deze verzameling geven we ook wel aan met D)
d-centrum	:	het middelpunt van de horizon
d-punt	:	punt van de disk
oneigenlijke punt	:	punt op de horizon
d-lijnen	:	[1] (Euclidische) cirkelboog op cirkels die de horizon loodrecht snijden, bestaande uit alle d-punten gelegen tussen de oneigenlijke punten [2] middellijn van de horizon met uitzondering van de oneigenlijke punten
d-lijnstuk	:	deel van een d-lijn bestaande uit alle punten tussen twee d-punten (inclusief beide d-punten, die eindpunten van het d-lijnstuk worden genoemd)
drager		de Euclidische cirkel waarvan een d-lijn of d-lijnstuk een boog is

Het stelsel [D, H] noemen we een hyperbolische meetkunde of ook wel het Poincaré-model van een hyperbolische meetkunde.
We geven deze meetkunde ookwel de naam P-meetkunde (de Euclidische meetkunde geven we soms aan met E-meetkunde).

We zullen een aantal eigenschappen van de P-meetkunde in hetgeen volgt onderzoeken (op de volgende pagina's).

figuur 4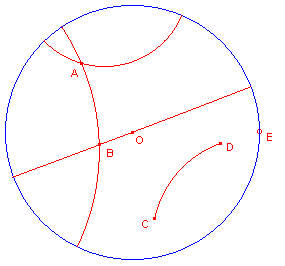

In de figuur hiernaast staan drie d-lijnen, twee door het punt A en twee door het punt B.
Het punt O, het d-centrum ligt op een d-lijn die door B gaat.
Het punt E (op de horizon) is een oneigenlijk punt.
CD is een d-lijnstuk.

Klik hier voor een animatie van een deel van deze figuur.

3. Twee stellingen (hyperbolisch)
Stellingen die direct samenhangen met de beide hulpstellingen en de H-afbeeldingen, zijn

Stellingen (hyperbolisch)
[1] Er is precies één H-afbeelding die een punt A waarin een richting a is vastgelegd afbeeldt op een punt B waarin een richting b is vastgelegd.
[2] Er is precies één H-afbeelding die een punt A op een punt B en tegelijk ook B op A afbeeldt (dubbelpunten).

Bewijs:
We merken vooraf op, dat Möbius-transformaties in het algemeen, en H-afbeeldingen dus in het bijzonder, conforme afbeeldingen zijn (hoektrouw; zie de pagina "Complex[3]").

figuur 5a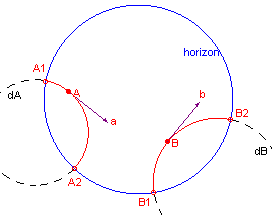

Bewijs van [1] (zie figuur 5a)
Volgens Hulpstelling 2 is er precies één orthogonaal cirkel (dA) door A rakend aan de richting a en precies één orthogonaal cirkel (dB) door B rakend aan de richting b.
Zij nu F de Möbius-transformatie die A₁,A,A₂ afbeeldt (in deze volgorde) op B₁,B,B₂. Deze afbeelding is uniek, immers een M-afbeelding wordt volledig bepaald door drie punten en hun beeldpunten; zie de pagina Complex[3]".
Wegens de conformiteit van F wordt nu dA afgebeeld op dB.

We zullen nu aantonen, dat F een H-afbeelding is.

F beeldt de cirkel die dA loodrecht snijdt in A₁ en A₂ (de horizon) af op een cirkel die dB loodrecht snijdt in B₁ en B₂ (de horizon).
(1.1)... De horizon wordt dus door F op zichzelf afgebeeld
A is een punt van D. F(A) = B is eveneens een punt van D.
(1.2)... D wordt dus op zichzelf afgebeeld (we behoeven dat maar voor éen punt te bewijzen!).
Uit (1.1) en (1.2) volgt dat F een H-afbeelding is. ¨

Gevolg van Stelling 1
Zij dA een orthogonaal cirkel door A (op de disk) en dB een orthogonaal cirkel door B (op de disk), dan zijn er twee H-afbeeldingen, waarbij A afgebeeld wordt op B en tevens dA op dB.

Bewijs:
Er zijn twee richtingen van de raaklijn in A aan dA.
Dus zijn er twee afbeeldingen, te weten A₁AA₂ >> B₁BB₂ en A₁AA₂ >> B₂AB₁ (hierbij betekent >>: "worden in deze volgorde afgebeeld op"). ¨

figuur 5b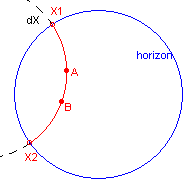

Bewijs van [2] (zie figuur 5b)
Zij dX de unieke cirkel door A en B die loodrecht staat op de horizon.
Nu is dX = dA = dB, zoals bedoeld in het Gevolg van Stelling 1.
Er zijn nu twee H-afbeeldingen: een afbeelding F₁ waarbij A >> B met dezelfde oriëntatie en een afbeelding F₂ waarbij A >> B met de omgekeerde oriëntatie.
F₁ kan B niet op A afbeelden omdat bij die afbeelding de oriëntatie op de cirkel wordt gehandhaafd.
We moeten dus aantonen dat F₂ het punt B ook op A afbeeldt.
Stel nu F₂(B) = A'.

We zullen nu aantonen, dat A' = A.
We hebben nu: F₂(X₁) = X₁ èn F₂(X₂) = X₂, maar hierbij wordt de oriëntatie gehandhaafd, zodat dit niet kan, OF
F₂(X₁) = X₂ èn F₂(X₂) = X₁.
Zoals bekend is de dubbelverhouding van vier punten invariant onder een M-afbeelding (zie de pagina "Complex[3]").
(X₁, X₂ ; A, B) = (X₂, X₁ ; B, A'), vanwege de afbeelding F₂.
Maar ook (X₁, X₂ ; A, B) = (X₂, X₁ ; B, A), een eigenschap van de dubbelverhouding.
Zodat (X₂, X₁ ; B, A') = (X₂, X₁ ; B, A), waaruit volgt dat A = A'.
En hiermee is de stelling bewezen. ¨

Begin

[hypm1.htm] laatste wijziging op: 03-06-2000