Complex bewijzen - 4
Overzicht ][ Complexe vlak | Meetkunde
10. (Generalisering
van de) Negenpuntscirkel ![]()
Zie ook de pagina "Over de cirkel van Feuerbach en de lijn
van Euler".
Zie ook de pagina "Euler-cirkels".
10.1. Negenpuntscirkel ![]()
We kiezen A, B, C op de eenheidscirkel; de affixen van zijn opvolgend a, b, c.
Hierdoor is |a| = |b| = |c| = 1.
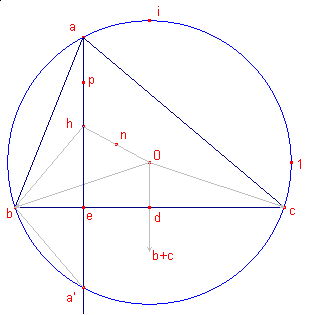 |
We stellen nu h = a + b + c (voor het punt H, dat nu nog geen hoogtepunt
is). Nu is h - a = b + c. Het punt H ligt dus op de loodlijn door A op BC, en wel zo, dat |h - a| = 2OD, immers d = (b+c)/2. H ligt ook op de loodlijn uit B op CA (h - b = a + c) en op de loodlijn uit C op AB (h - c = a + b). h is dus de affix van het hoogtepunt van driehoek ABC. Zij nu N het midden van OH, met n = ½.h = ½(a+b+c). ND = |n - d| = |½(a+b+c) - ½(b+c)| = |a|/2 = ½. Ook de afstand van N tot het midden van beide andere zijden is dan ½. ## N is dus het middelpunt van de cirkel door de middens van de zijden van de driehoek. Zij p (de affix van) het midden van AH. Dus p = (a + h)/2. |
a' is (de affix van) het tweede snijpunt van de hoogtelijn uit a met cirkel abc.
aa' _|_ bc. Dus (a - a') / (b - c) is imaginair.
Zodat ![]()
Vervangen we hierin a_ door 1/a, dan krijgen we:
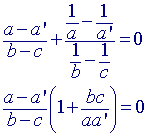
zodat 1 + bc/aa' = 0, waaruit we vinden a' = -bc/a.
Nu is
BA' = |b + bc/a| = |b/a|.|a+c| = |a+c|
BH = |b - (a+b+c)| = |-a-c| = |a+c|.
Driehoek BHA' is gelijkbenig. Voor het midden E (met affix e) van HA' hebben we dan:
e = ½(h + a') = ½(h - bc/a)
NE = |½h - ½h + (bc)/(2a)| = (|b|.|c| / (2|a|) = ½.
## De bedoelde cirkel gaat dus ook door de voetpunten van de hoogtelijnen
van de driehoek.
| Stelling 11 Van een driehoek liggen de middens van de zijden, de middens van de bovenste hoogtelijnstukken en de voetpunten van de hoogtelijnen (op de zijden) op een cirkel (negenpuntscirkel of cirkel van Feuerbach). |
Samengevat
We hebben nu in een willekeurige driehoek A1A2A3
op de eenheidscirkel de volgende relaties:
| middelpunt | = | 0 |
| zwaartepunt | = | 1/3(a1 + a2 + a3) |
| middelpunt negenpuntscirkel | = | 1/2(a1 + a2 + a3) |
| hoogtepunt | = | a1 + a2 + a3 |
| straal omcirkel | = | 1/2 |
Zie ook Pagina 5 (Over bissectrices) voor de Stelling van Feuerbach.
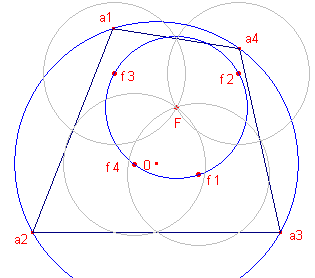 |
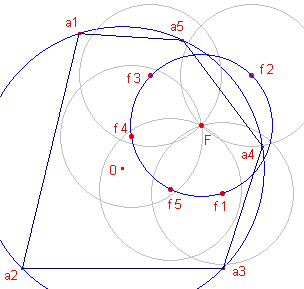
We gaan nu uit van vier punten Ai (i = 1, 2, 3, 4) op
de eenheidscirkel. Kiezen we telkens drie punten hieruit, dan krijgen we vier driehoeken (die alle de eenheidscirkel als omcirkel hebben). We vinden voor de negenpuntscentra Fj met affix fj:
|
Voor het punt F met affix f = 1/2(a1
+ a2 + a3 + a4) geldt nu:
|f - f1| = |f - f2| = |f - f3| = |f - f4|
= 1/2
De negenpuntscirkels van de genoemde driehoeken gaan dus alle door het punt F, maw. de
punten Fj liggen op een cirkel met middelpunt F en straal 1/2.
Deze cirkel wordt wel de Euler-cirkel van A1A2A3A4
genoemd. Het middelpunt van de cirkel heet wel het Euler-punt van de
vierhoek.
Klik hier ![]() voor een CabriJavapplet
bij het bovenstaande.
voor een CabriJavapplet
bij het bovenstaande.
Opmerking
Zie ook de pagina "Euler-cirkels" op
deze website.
Daar wordt een meer meetkundige behandeling van bovenstaande en volgende eigenschap
gegeven.
Zie ook de pagina "Koordenvierhoeken", paragraaf 2.2.2. Voetpuntsrechten en negenpuntscirkels.
[einde Opmerking]
11. Referenties
![]()
[1] J.L. Coolidge, A treatise on the circle and the sphere, Chelsea Publishing
Company (New York, 1971)
[2] Liang-shin Hahn: Complex
Numbers and Geometry, MAA, 1994
[3] M. Koecher, A. Krieg: Ebene Geometrie, Springer Verlag, 2000
[4] Wells, D: The Penguin Dictionary of Curious and Interesting Geometry,
Penguin (Londen, 1991)
[5] Y.M. Yaglom, Geometric Transformations II, Random House (New York, 1968)
¤ Klik hier voor de volgende pagina
![]()
[bewijs4.htm] laatste wijziging op: 12-05-02