Gergonne-lijn, Nobbs-punten

Gergonne-lijn | Nobbs-punten ][ Gergonne-driehoek

Gergonne-lijn

Stelling 1
Als P ligt op de poollijn van Q (t.o.v. een cirkel / kegelsnede), dan ligt Q op de poollijn van P.

Dit is de zogenoemde hoofdstelling van de pooltheorie (ook wel de stelling van De la Hire, naar Philippe de la Hire, 1640-1718, Frankrijk).

Stelling 2
De verbindingslijnen van de hoekpunten van een driehoek met de raakpunten van de incirkel aan de zijden van die driehoek, zijn concurrent.

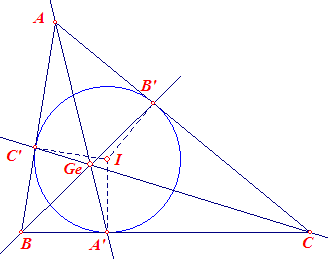Het bedoelde punt is het zogenoemde Gergonne-punt van de driehoek (naar Joseph Diaz Gergonne, 1771-1859, Frankrijk).
Zie ook de pagina "Gergonne-punt, Gergonne-driehoek".

In de figuur hiernaast:
   Ge = Gergonne-punt (zie ook: Kimberling-classificatie X7)
   I = incentrum (zie ook: Kimberling-classificatie: X1)
   A'B'C' = Gergonne-driehoek

Stelling 3
De snijpunten van de zijden van de driehoek en de 'overeenkomstige' zijden van de Gergonne-driehoek zijn collineair.
De collineatie-as heet Gergonne-lijn. De snijpunten heten de Nobbs-punten van de basisdriehoek.

Eerste bewijs:
Klik hier >< voor een CabriJavapplet die stelling 3 illustreert.

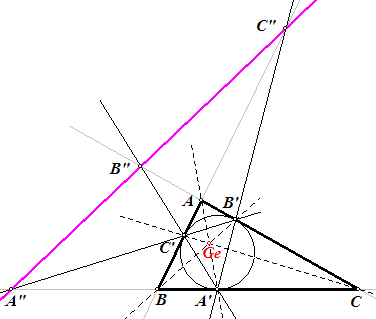In nevenstaande figuur hebben we:
   A', B', C' - raakpunten van de incirkel aan de zijden van ABC;
   B'C', C'A', A'B' - verbindingslijnen van twee raakpunten;
   A", B", C" - Nobbs-punten;
   A"B"C" - Gergonne-lijn.

De lijnen AC' en AB' zijn raaklijnen aan de incirkel (I).
B'C' is de poollijn van A tov. (I).
A" ligt op de poollijn van A, dus A ligt op de poollijn van A" ......(i, zie stelling 1)
A' is het raakpunt van een raaklijn uit A" aan (I). Dus:
A' ligt op de poollijn van A" ......(ii)
Uit (i) en (ii) volgt:
AA' is de poollijn van A" tov. (I)
Ge ligt op de poollijnen van A", B", C", dus A", B", C" liggen op de poollijn van Ge (de Gergonne-lijn); weer volgens stelling 1.
Dus ook:
De Gergonne-lijn is de poollijn van het Gergonne-punt tov. de incirkel.¨

Opmerking
De naam 'Gergonne-lijn' is voor het eerste gebruikt door Adrian Oldknow in:
A. OLDKNOW: The Euler-Gergonne-Soddy Triangle of a Triangle. In: The American Mathematical Monthly 103 (1996), pp. 319-329.
Zie ook:
ERIC W. WEISSTEIN: "Gergonne Line." From MathWorld -- A Wolfram Web Resource. http://mathworld.wolfram.com/GergonneLine.html
[einde Opmerking]

Tweede bewijs:
De driehoeken ABC (de basisdriehoek) en A'B'C' (de Gergonne-driehoek) zijn puntperspectief (perspectiefcentrum is Ge).
Volgens de stelling van Desargues zijn de driehoeken dan ook lijnperspectief.
De snijpunten van overeenkomstige zijden, A" = BC/\B'C', B" = CA/\C'A', C" = AB/\A'B' zijn dus collineair.
Waarmee de stelling eveneens bewezen is.¨

Definitie
De lijn IGe, de verbindingslijn van het incentrum I en het Gergonne-punt Ge, heet de Soddy-lijn van driehoek ABC.

Zie verder ook de pagina "Soddy-cirkels". De Soddy-lijn is genoemd naar Sir Frederick Soddy (1877-1956, Engeland).

Stelling 4
De Soddy-lijn van een driehoek staat loodrecht op de Gergonne-lijn van die driehoek.

Bewijs:

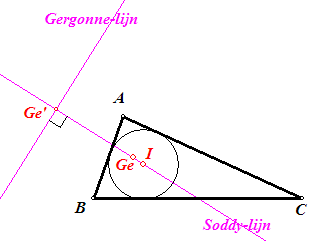Ge is de pool van de Gergonne-lijn tov. de incirkel (zie stelling 3, eerste bewijs).

De poollijn p van een punt P tov. een cirkel (O, k) wordt gedefinieerd als de loodlijn door het punt P' op de lijn OP met OP · OP' = k²; zie de pagina "Pool en poollijn tov. een cirkel".

De stelling volgt dus direct uit die definitie.¨

[p : gergonne.htm] laatste wijziging op: 23-07-2005