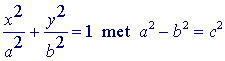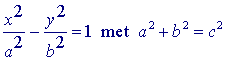Kegelsneden en hun vergelijkingen

Overzicht  ][  Anal. meetkunde | Meetkunde

Zie ook: Kegelsneden volgens Apollonius
Zie ook: Pooltransformaties
Zie ook: Parabolen: meetundige eigenschappen en constructies
Zie ook: Ellips-constructies met Cabri
Zie ook: Bollen van Dandelin

0. Overzicht begin pagina

  1. Parabool cabrisignal
  2. Ellips cabrisignal
  3. Hyperbool cabrisignal
  4. Brandpuntsvoerstralen, Richtlijnen en excentriciteit
         4.1. Ellips
         4.2. Hyperbool
         4.3. Parabool
  5. Kegelsneden cabrisignal
  6. Kegelsneden als doorsnede van een kegel met een vlak (een animatie)

1. Parabool begin pagina

Definitie
Een parabool is de meetkundige plaats van de punten waarvoor de afstand tot een gegeven punt F (het brandpunt) gelijk is aan de afstand tot een gegeven lijn l (de richtlijn).

Klik hier Animatie voor een animatie bij deze definitie.

Vastlegging coördinatenstelsel
x-as: lijn door F loodrecht op op l
y-as: door het midden van de afstand FA tussen F en l. Stel deze afstand gelijk aan p (de parameter van de parabool).

Afleiding vergelijking

figuur 1  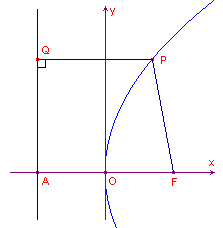kever1 Nu is A(-½p, 0) en  F(½p, 0)

Stel P(x, y).

Dan is

PF = Ö( (x - ½p)2 + y2 )
PQ = | x + ½p |

Op basis van de definitie: PF = PQ, vinden we

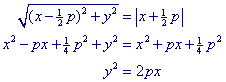
imageskever_f1

Vergelijking parabool:   y2 = 2px

¤ Zie ook: Parabolen: meetundige eigenschappen en constructies

2. Ellips begin pagina

Definitie
Een ellips is de meetkundige plaats van de punten met de eigenschap dat de som van de afstanden tot twee vaste punten F1 en F2 (de brandpunten) constant is.

Klik hier Animatie voor een animatie bij deze definitie.

Vastlegging coördinatenstelsel
x-as: de lijn door F1 en F2
y-as: door het midden van de afstand F1F2. Stel deze afstand gelijk aan 2c.

Afleiding vergelijking

figuur 2  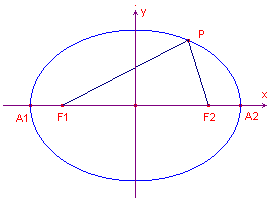kever2 We stellen de vaste afstand (uit de definitie) gelijk aan 2a.

Nu is F1(-c, 0) en F2(c, 0).

Stel P(x, y).

Dan is

PF1 = Ö( (x + c)2 + y2 )
PF2 = Ö( (x - c)2 + y2 )

Op basis van de definitie PF1 + PF2 = 2a hebben we dan
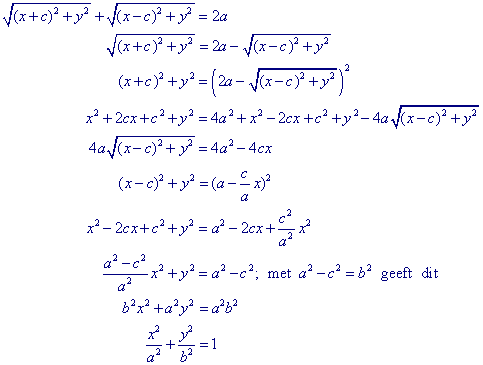
imageskever_f2

Vergelijking:    imageskever_f3

¤ Zie ook: Ellips-constructies met Cabri

3. Hyperbool begin pagina

Definitie
Een hyperbool is de meetkundige plaats van de punten met de eigenschap dat het verschil van de afstanden tot twee vaste punten F1 en F2 (de brandpunten) constant is.

Klik hier Animatie voor een animatie bij deze definitie.

Vastlegging coördinatenstelsel
x-as: de lijn door F1 en F2
y-as: door het midden midden vab het lijnstuk F1F2. Stel deze afstand gelijk aan 2c.

Afleiding vergelijking

figuur 3  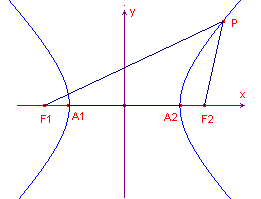kever3 We stellen de vaste afstand (uit de definitie) gelijk aan 2a.

Nu is F1(-c, 0) en F2(c, 0).

Stel P(x, y).

Dan is

PF1 = Ö( (x + c)2 + y2 )
PF2 = Ö( (x - c)2 + y2 )

Op basis van de definitie | PF1 - PF2 | = 2a    hebben we dan
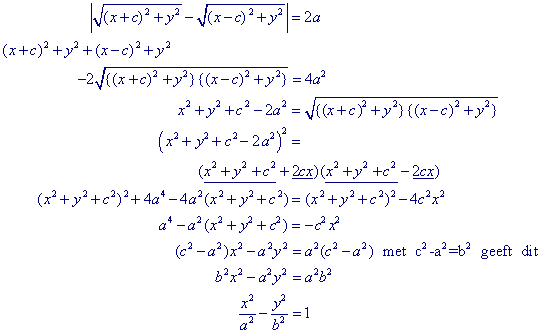
imageskever_f4

Vergelijking:    imageskever_f5

4. Brandpuntsvoerstralen, richtlijnen en excentriciteit begin pagina

4.1. Ellips begin pagina
Zie figuur 4 waarin d1 = PF1 en d2 = PF2 de (brandpunts)voerstralen zijn.
We hebben nu PF12 = d12 = (x + c)2 + y2 en d22 = (x - c)2 + y2.

figuur 4  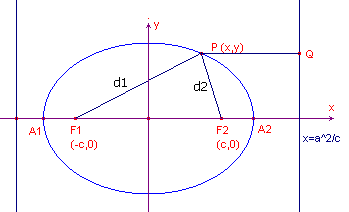kever4 Nu is
   d12 - d22 = 4cx
en (uit de definitie)
(1).....   d1 + d2 = 2a
zodat
(2).....   d1 - d2 = 2cx / a
Uit (1) en (2) volgt dan eenvoudig
   d2 = a - cx/a, d1 = a + cx /a
We bekijken nu alleen de uitdrukking voor d2 (voor d1 kunnen we eenzelfde redenering opzetten).

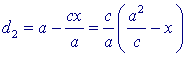
imageskever_f6
In figuur 4 is (rechts) een lijn getekend met vergelijking x = a2/c.
Deze lijn is een richtlijn van de ellips.
De meetkundige betekenis van de tweede factor van het product voor d2 kunnen we eenvoudig inzien: PQ = a2/c - x
Zodat dus PF2 = d2 = c/a . PQ
Zodat PF2 / PQ = c /a
Het getal c /a (dat kleiner is dan 1, omdat c < a) heet de excentriciteit van de ellips.
We kunnen dus vaststellen:

Stelling 1
Een ellips is de meetkundige plaats van de punten waarvoor de afstand tot een vast punt (brandpunt) en de afstand tot een vaste rechte lijn (richtlijn) een constante verhouding kleiner dan 1 hebben.

Opmerkingen
[1]
Zie de pagina "Twee raaklijnen aan een ellips" voor een meetkundige behandeling van (oa.) de orthoptische cirkel van een ellips.
[2]
Zie de pagina "Toegevoegde middellijnen" waarop enkele andere meetkundige aspecten van de ellips worden behandeld.
[3]
Op de pagina "Ellips-constructies met Cabri" wordt een aantal constructies van de ellips (inclusief bewijzen) behandeld.
[4]
Zie ook de pagina "Over de richtlijnen van een ellips" voor enkele meetkundige eigenschappen van de richtlijn(en).
[einde Opmerkingen]

4.2. Hyperbool begin pagina
In figuur 5 zijn d1 en d2 de brandpuntsvoerstralen van de hyperbool.
We kiezen het punt P op de rechter tak van de hyperbool.
We hebben nu:

figuur 5  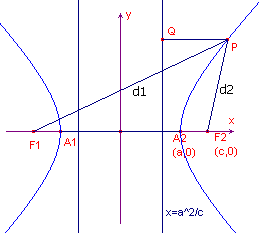kever5 PF12 = d12 = (x + c)2 + y2 en d22 = (x - c)2 + y2.
Zodat
   d12 - d22 = 4cx
en (uit de definitie)
(1).....   d1 - d2 = 2a
zodat
(2).....   d1 + d2 = 2cx / a
Uit (1) en (2) volgt nu eenvoudig
   d2 = cx /a -a
We behandelen verder alleen d2 (voor d1 kan eenzelfde redenering worden opgezet).

Voor d2 kunnen we weer schrijven
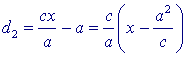
imageskever_f7
In figuur 5 is (rechts van de oorsprong) een lijn getekend met vergelijking x = a2/c.
Deze lijn is een richtlijn van de hyperbool.
De meetkundige betekenis van de tweede factor van het product voor d2 kunnen we eenvoudig inzien: PQ = x - a2/c.
Zodat dus PF2 = d2 = c/a . PQ
Zodat PF2 / PQ = c /a
Het getal c /a (dat groter is dan 1, omdat c > a) heet de excentriciteit van de hyperbool.
We kunnen dus vaststellen

Stelling 2
Een hyperbool is de meetkundige plaats van de punten waarvoor de afstand tot een vast punt (brandpunt) en de afstand tot een vaste rechte lijn (rictlijn) een constante verhouding groter dan 1 hebben.

4.3. Parabool begin pagina

figuur 5  kever1 Ook bij de parabool (zie figuur 5) noemen we PF de brandpuntsvoerstraal.
Nu is (per definitie): PF / PQ = 1
We zeggen daarom dat de excentriciteit van een parabool gelijk is aan 1.

In de definitie van de parabool wordt de richtlijn zelf al gebruikt. We kunnen die definitie dus ook formuleren als gedaan is (in stellingen) voor de ellips en de hyperbool:

Stelling 3
Een parabool is de meetkundige plaats van de punten waarvoor de afstand tot een vast punt (brandpunt) en de afstand tot een vaste lijn (richtlijn) een constante verhouding gelijk aan 1 hebben.

¤ Zie ook: Parabolen: meetundige eigenschappen en constructies

5. Kegelsneden begin pagina
Op grond van stelling1, stelling 2 en stelling 3 kunnen we dus samenvatten

Stelling 4
Iedere kegelsnede is te beschouwen als de meetkundige plaats van die punten waarvoor de afstand tot een vast punt (brandpunt) en de afstand tot een vaste lijn (richtlijn) een constante verhouding e (excentriciteit) hebben.
Als e < 1 dan is de kegelsnede een ellips, voor e = 1 een parabool, terwijl ze een hyperbool is voor e > 1.
.
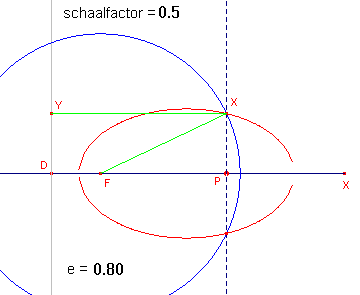kever6 Klik hier Animatie voor een CabriJavapplet ter illustratie van Stelling 4 (de figuur hiernaast geeft op basis van de waarde e =0.80  bij de gegeven punten F en D (het voetpunt van de richtlijn) een ellips).

Zie in dit verband ook de animatie op de pagina "Pooltransformatie" waarbij via polariteiten een cirkel kan worden afgebeeld op een ellips, parabool en hyperbool.

6. Kegelsneden als doorsnede van een kegel en een vlak begin pagina
Het directe verband tussen ellips, parabool en hyperbool kan inzichtelijk worden gemaakt door een kegel te snijden met een plat vlak..
Zie voor een animatie hiervan de pagina "Kegelsneden-animatie".
Zie ook de pagina "Kegelsneden volgens Apollonius".

up
[kever.htm] laatste wijziging op: 08-11-2003