De functie f(x) = ax + b

Overzicht  ][  Analyse

0. Overzicht begin pagina

  1. De grafiek van de functie cabrisignal
  2. Rechte lijn bepaald door een punt en de rico
  3. Rechte lijn bepaald door twee punten
  4. Rechte lijn gaande door een punt en evenwijdig met een tweede lijn
  5. Rechte lijnen evenwijdig met de y-as
  6. De coördinaatsassen

1. De grafiek van de functie begin pagina
De functie f(x) = ax + b (met a en b reële getallen) heet lineaire functie (eerste-graads functie).
Het getal a heet de richtingscoëfficiënt (rico, r.c.) van de functie.

Stelling
De grafiek van de functie f(x) = ax + b is een rechte lijn.

Bewijs:
a = 0
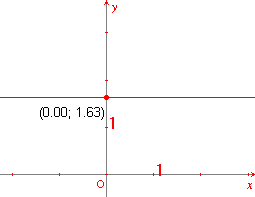
Het functievoorschrift luidt nu: f(x) = b.
De grafiek van de functie is een rechte lijn, immers voor alle punten (x, y) = (x , b) geldt dat de afstand tot de x-as gelijk is aan |b|.
De grafiek is dus evenwijdig aan de x-as.

figuur 1a        figuur 1b
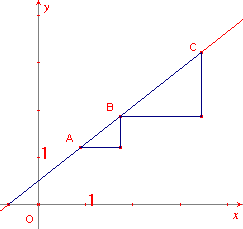
linfunc1 linfunc2

a ¹ 0
Zie figuur 1b.
Zijn A(x1, ax1 + b), B(x2, ax2 + b) en C(x3, ax3 + b) drie punten met coördinaten (x, y) die voldoen aan y = ax + b.
Zonder de algemeenheid geweld aan te doen kunnen we stellen x1 < x2 < x3.
Voor de tangenten van de hoeken die de lijnen AB en AC met de (positieve) x-as maken, geldt:
tan(AB) = (ax2 + b - ax1 - b) / (x2 - x1) = a(x2 - x1) / (x2 - x1) = a
tan(AC) = (ax3 + b - ax1 - b) / (x3 - x1) = a(x3 - x1) / (x3 - x1) = a
De lijnen zijn dus evenwijdig. Omdat ze beide door A gaan vallen ze samen.

De punten van de grafiek van de functie f(x) = ax + b liggen dus op een rechte lijn.
Of, de grafiek van de functie f(x) = ax + b is een rechte lijn. ¨

Opmerking
De uitdrukking y = ax + b heet een vergelijking van de rechte lijn.
Het getal a heet de richtingscoëfficiënt van de rechte lijn.
[einde Opmerking]

Klik hier Animatie voor een animatie waarin de functie kan worden getekend voor verschillende waarden van a en b.

In de paragraaf 2, paragraaf 3 en paragraaf 4 wordt (met voorbeelden) het vinden van een vergelijking van een lijn behandeld op basis van verschillende gegevens.

2. Rechte lijn bepaald door een punt en de rico begin pagina

Voorbeeld Bepaal een vergelijking van de rechte lijn die gaat door het punt (1,3) met rico = 4.
Oplossing: De algemene vergelijking is: y = ax + b
De rico is 4, dus: y = 4x + b
Het punt (x,y) = (1,3) ligt op de lijn, dus moet gelden 3 = 4.1 + b
Of 3 = 4 + b, waaruit volgt: b = -1.
Een vergelijking is dus:
y = 4 x - 1

3. Rechte lijn bepaald door twee punten begin pagina

Voorbeeld Bepaal een vergelijking van de rechte lijn die gaat door de punten (1, 3) en (6,2).
Oplossing: Voor de rico geldt: rico = (2 - 3) / (6 - 1) = - 1/5.
We hebben dus: y = - 1/5 x + b
We gebruiken nu éen van de twee punten om de waarde van b te berekenen.
Voor (x,y) = (1, 3) hebben we: 3 = - 1/5 + b.
Dus b = 3 1/5.
Een vergelijking is dan:
y = - 1/5 x + 3 1/5

4. Rechte lijn gaande door een punt en evenwijdig met een tweede lijn

Voorbeeld Bepaal een vergelijking van de rechte lijn door het punt (1,3) die evenwijdig is met de lijn met vergelijking x + 5 y = 12.
Oplossing: Uit de vergelijking x + 5y = 12 volgt de rico van deze lijn. We schrijven de vergelijking in de vorm y = ...:
5 y = - x + 12
y = - 1/5 x + 12/5
De rico van deze lijn, en ook die van de gezochte, is - 1/5 .
We hebben dus voor de gezochte lijn y = - 1/5 x + b.
Op dezelfde manier als in paragraaf 3 vinden we dan
y = - 1/5 x + 3 1/5

5. Rechte lijnen evenwijdig met de y-as begin pagina
Rechte lijnen evenwijdig met de y-as zijn geen grafieken van functies!!
Immers, bij functies hoort bij elke x hoogstens éen waarde van y.
Daardoor hebben deze lijnen geen richtingscoëfficiënt.
Bij een rechte lijn die evenwijdig is met de y-as, kunnen we wel een vergelijking vinden:
   x = p
Hierbij is (p, 0) het snijpunt van de lijn met de x-as.

6. De coördinaatsassen begin pagina
Uit het bovenstaande (paragraaf 1 en paragraaf 5) volgt:
een vergelijking van de x-as is: y = 0
een vergelijking van de y-as is: x = 0

begin pagina
[linfunc.htm] laatste wijziging op: 18-11-02