Proposities I-16, I-18, I-19, I-32

1. Inleiding
We bewijzen de volgende stellingen:

Stelling 1
Zijn twee hoeken van een driehoek ongelijk, dan ligt tegenover de grootste van die hoeken een grotere zijde dan tegenover de kleinste.

Stelling 2
Een buitenhoek van een driehoek is gelijk aan de som van de beide niet-aanliggende binnenhoeken van die driehoek

Opmerking
Stelling 1 staat op de pagina over de driehoeksongelijkheid genoemd als stelling 3. Op deze stelling is het daar staande bewijs van de driehoeksongelijkheid gebaseerd.
Stelling 2 wordt ook gebruikt in het genoemde bewijs van de driehoeksongelijkheid.
Kortom, beide stellingen zijn nodig om de driehoeksongelijkheid te bewijzen.
[einde Opmerking]

We geven het bewijs van deze stellingen op zoals ze voorkomen in de Elementen van Euclides.
We beginnen met een iets beperkte formulering van stelling 2.

Propositie I-16
In elken driehoek is, wanneer een zijde verlengd is, de buitenhoek grooter dan elk der afgelegen binnenhoeken
(zie noot 1).

Zij ABC een driehoek en laat een zijde ervan, BC, verlend zijn tot het punt D (zie figuur 1).

figuur 1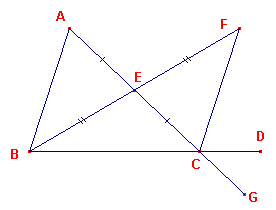

Ik zeg dat de buitenhoek ACD groter is dan elk van de afgelegen binnenhoeken CBA, BAC.

Laat AC in twee gelijke delen verdeeld zijn in E en laat BE verbonden zijn en verlengd in een rechte lijn tot F:
laat EF gelijk gemaakt zijn aan BE, laat FC verbonden zijn en laat AC getrokken zijn naar G.

Dan zijn opvolgend, omdat AE gelijk is aan EC, en BE aan EF, de twee zijden AE, EB opvolgend gelijk aan de zijden CE, EF;
en de hoek AEB is gelijk aan de hoek FEC, omdat het overstaande hoeken zijn.

Daarom is de basis AB gelijk aan de basis FC, en de driehoek ABE is gelijk aan (congruent met) de driehoek CFE, en de overblijvende hoeken zijn opvolgend gelijk aan de overblijvende hoeken, namelijk de aanliggende aan de gelijke zijden; daarom is de hoek BAE gelijk aan de hoek ECF.

Maar de hoek ECD is groter dan de hoek ECF;
daarom is de hoek ACD groter dan de hoek BAE.

Op dezelfde manier ook, als BC in twee gelijke delen wordt verdeeld, kan bewezen worden dat de hoek BCG, dat is de hoek ACD, groter is dan de hoek ABC.

Daarom is hoek ACD groter dan elk van de afgelegen binnenhoeken CBA, BAC.

Hetgeen te bewijzen was. ¨

2. Commentaar
De reden voor het opnemen van Propositie I, 16 op deze pagina is dat bovenstaande stelling geheel onafhankelijk is van het 5e postulaat van Euclides (parallellenpostulaat), en omdat men deze eigenschap vaak uit stelling 2 (die in de Elementen wordt bewezen in Propositie I, 32) laat volgen.
We geven hieronder het commentaar bij propositie I, 16 weer van Dr. E.J. Dijksterhuis (zie noot 1).

Deze propositie (Prop. I, 16; DK), die bij het bewijs van verschillende stellingen een rol zal blijken te spelen, komt bij de wijze, waarop men in onzen tijd de elementaire wiskunde behandelt, veelal in het geheel niet meer tot haar recht. Men beschouwt haar namelijk als een gevolg van de stelling, dat een buitenhoek van een driehoek gelijk is aan de som van de niet-aanliggende binnenhoeken, welke zelf aequivalent is met de stelling, dat de som van de hoeken van een driehoek gelijk is aan twee rechte hoeken.
Het is duidelijk, dat dit uit axiomatisch oogpunt een ernstige fout is; immers de stelling van de hoekensom steunt op het vijfde postulaat, terwijl propositie I, 16 daarvan onafhankelijk is.We ontmoeten hier een sprekend voorbeeld, hoezeer de moderne elementaire meetkunde menigmaal in systematiek van opbouw bij het oorspronkelijke werk van Euclides achterstaat.

Het in onzen tijd door de verkeerde behandeling in de schoolboeken menigmaal verduisterde inzicht in de ware beteekenis van de stelling van de buitenhoek is in volle scherpte aanwezig bij de voorlopers en de grondleggers der niet-Euclidische meetkunde. Wie b.v. de werken van Saccheri en Lobatchevsky raadpleegt, merkt al spoedig, welk een zeer belangrijke rol zij in hunne redeneeringen speelt. Dit is begrijpelijk; de proposities I, 1-27 van Euclides zijn onafhankelijk van het vijfde postulaat en gelden dus in de hyperbolische meetkunde; de propositie I, 16 (met haar corollarium I, 17, dat de som van twee hoeken van een driehoek kleiner is dan twee rechte) is dan echter de eenige algemeene stelling, die men, zonder op de zijden te letten, over het verband van de hoeken van een driehoek kan uitspreken.

3. Stelling 1, propositie I-18 en propositie I-19
We bewijzen nu Stelling 1, die in de Elementen voorkomt als Propositie I, 19. Daaraan voorafgaand is het gezien de logische opbouw verstandig om eerst naar propositie 1, 18 te kijken.

Propositie I-18
In elken driehoek onderspant de grootere zijde den grooteren hoek
(zie noot 1).

Zij ABC een driehoek waarvan de zijde AC groter is dan AB (zie figuur 2).

Ik zeg dat de hoek ABC ook groter is dan de hoek BCA.

Laat nu, daar AC groter is dan AB, AD gelijk gemaakt zijn aan AB en laat BD verbonden zijn.
Daar de hoek ADB een buitenhoek is van de driehoek BCD, is deze [hoek] groter dan de niet-aanliggende binnenhoek DCB [I, 16].
Maar de hoek ADB is gelijk aan de hoek ABD, omdat de zijde AB gelijk is aan AD;
daarom is de hoek ABD ook groter dan de hoek ACB;
daarom is de hoek ABC veel groter dan de hoek ACB.

figuur 2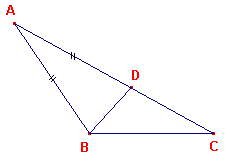

Daarom is de hoek ABC groter dan de hoek BCA.

Hetgeen te bewijzen was.¨

Propositie I-19
In elken driehoek spant zich onder den grooteren hoek de grootere zijde
(zie noot 1).

Laat ABC een driehoek zijn met de hoek ABC groter dan de hoek BCA (zie ook figuur 2).

Ik zeg dat de zijde AC ook groter is dan de zijde AB.

Want, als dat niet zo is, dan is AC òf gelijk aan AB òf kleiner.
Nu is AC niet gelijk aan AB; want dan zou de hoek ABC gelijk zijn aan de hoek ACB; maar dat is niet zo.
Daarom is AC niet gelijk aan AB.
Ook niet is AC kleiner dan AB; want dan zou de hoek ABC kleiner zijn dan de hoek ACB [I, 18]; maar dat is niet zo;
Daarom is AC niet kleiner dan AB.
En het was bewezen dat hij ook niet kleiner was dan AB

Daarom is AC groter dan AB.

Hetgeen te bewijzen was. ¨

4. Stelling 2, propositie I-32
De hierboven gegeven stelling 2) wordt in de Elementen bewezen als onderdeel van de stelling over de som van de hoeken van een driehoek. We hebben

Propositie I-32
In elken driehoek is, wanneer een der zijden verlengd is, de buitenhoek gelijk aan de twee afgelegen binnenhoeken en de drie binnenhoeken van den driehoek zijn gelijk aan twee rechte
(zie noot 1).

Zij ABC een driehoek, en zij een zijde ervan, BC, verlengd tot D (zie figuur 3).

Ik zeg dat de buitenhoek ACD gelijk is aan de [som van de] twee afgelegen binnenhoeken CAB, ABC, en [dat de som van] de drie binnenhoeken van de driehoek ABC, BCA, CAB gelijk is aan twee rechte hoeken.

Want laat CE door het punt C evenwijdig getrokken zijn met de rechte lijn AB.

figuur 3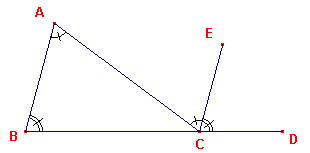

Omdat AB evenwijdig is met CE en AC beide snijdt, zijn de verwisselende binnehoeken BAC, ACE aan elkaar gelijk.
Weer, omdat AB evenwijdig is met CE en BD beide snijdt, is de buitenhoek ECD gelijk aan de niet-aanliggende binnenhoek ABC.
Maar bewezen was, dat de hoek ACE gelijk ias aan de hoek BAC; daarom is de gehele hoek ACD gelijk aan de beide afgelegen binnenhoeken BAC, ABC.

Let nu de hoek ACB opgeteld worden bij beide; daarom zijn de hoeken ACD, ACB gelijk aan de drie hoeken ABC, BCA, CAB.
Maar de hoeken ACD, ACB zijn gelijk aan twee rechte hoeken; daarom zijn de hoeken ABC, BCA, CAB ook gelijk aan twee rechte hoeken.

Hetgeen te bewijzen was. ¨

noot 1
De vertaling uit het Grieks van de tekst van de proposities I-16, I-18, I-19 en I-32 en het commentaar bij propositie I-16 zijn overgenomen uit Dr. E.J. Dijksterhuis, De Elementen van Euclides, P. Noordhoff, Groningen, 1929.
De bewijzen van de proposities zijn uit het Engels vertaald uit Th. L. Heath, The Thirteen Books of Euclid's Elements, Dover Publications, Inc., New York, 1956 (2nd edition).

[propI16.htm] laatste wijziging op: 26-03-1999