Afstanden

Definitie en stellingen | Kruisende lijnen ][ Overzicht stereo | Meetkunde | Cabri 3D

1. Definitie, en stellingen over punt-vlak, lijn-vlak, vlak-vlak

Definitie
Onder de afstand van twee figuren verstaan we de kleinste lengte van een lijnstuk dat een punt van de ene figuur met een punt van de andere figuur verbindt.

Nb.
Voor figuren die in hetzelfde vlak liggen, worden de definities uit de vlakke meetkunde (planimetrie) gebruikt.

Stelling 1
De afstand van een punt tot een vlak is de lengte van het loodlijnstuk uit dat punt op het vlak.

Bewijs:

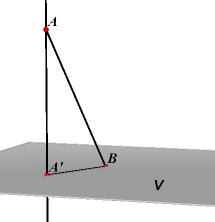Is AA' loodrecht op V en is B een van A' verschillend punt in V, dan is AB > AA', immers AB is de schuine zijde in de in A' rechthoekige driehoek AA'B.¨

Stelling 2
De afstand van een lijn tot een daaraan evenwijdig vlak is de lengte van het loodlijnstuk uit een punt van die lijn op het vlak.

Bewijs:

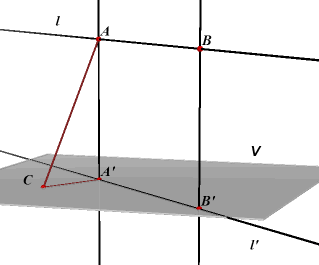De lijn l is evenwijdig met V.

1. Twee loodlijnstukken uit de punten AA' en BB' van l op V zijn gelijk.
Want
l // V geeft l // l'
en AA' _|_ V. BB' _|_ V geeft AA' // BB'.
Zodat AA'B'B een parallellogram (rechthoek) is, waaruit volgt dat AA' = BB'.

2. Is AC een ander verbindingslijnstuk van l en V, dan is AC > AA', want AC is schuine zijde in de in A' rechthoekige driehoek AAC¨.

Stelling 3
De afstand van twee evenwijdige vlakken is de lengte van een loodlijnstuk uit een punt van het ene vlak op het andere vlak.

Bewijs:
Het bewijs verloop analoog aan dat van stelling 2.¨

2. Afstand van twee kruisende lijnen
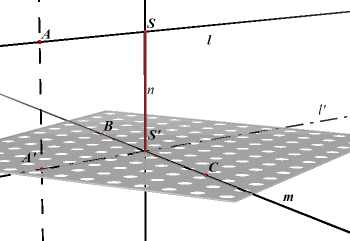
We vinden de afstand van twee kruisende lijnen l en m als volgt::

- Breng door de lijn m een vlak V aan dat evenwijdig is met l.
- Projecteer l op V. Noem de projectie l'.
- Richt in het snijpunt S' van l' en m een loodlijn n op op V. De lijn n snijdt l in het punt S.

Stelling 4
Het lijnstuk SS' (zoals hierboven beschreven) is de afstand van l en m.

Bewijs:

Het lijnstuk SS' is inderdaad de afstand tussen l en m. Want elk andere lijnstuk a is ook verbindingslijnstuk tussen l en V. En dan is (zie stelling 2) a groter of gelijk aan SS'.¨

Gevolg
De gevonden lijn n snijdt de lijnen l en m loodrecht (gemeenschappelijke loodlijn). Immers:
Uit SS' _|_ V volgt dat SS' _|_ m en dat SS' _|_ l'.
Maar l // V geeft l // l', zodat SS' _|_ l.¨

Klik hier >< voor een Cabri 3D applet bij nevenstaande figuur (opent in een NieuwVenster).

Opmerking
We kunnen ook bewijzen dat de lijn n de enige lijn is die l en m loodrecht snijdt.
Bewijs:
Stel ook een lijnstuk TT' snijdt de lijnen l en m loodrecht.
Dan geldt: TT' _|_ l, en dus TT' _|_ l'.
Omdat TT' _|_ m hebben we TT' _|_ V. Maar ook SS' _|_ V, zodat de dragers van SS' en TT' evenwijdig zijn. SS' en TT' liggen dan in hetzelfde vlak W.
S en T liggen op l en S' en T' liggen op m. De lijnen l en m liggen dan ook in W. En dat is in tegenspraak met het feit dat l en m elkaar kruisen.¨

Zodat bewezen is:

Stelling 5
Er is precies één lijn die twee gegeven kruisende lijnen loodrecht snijdt.

[p ; afstanden.htm] laatste wijziging op: 01-10-2008