Half-gelijkzijdig en gelijkzijdig viervlak

Half-gelijkzijdig viervlak | Gelijkzijdig viervlak ][ Overzicht stereo | Cabri 3D

Half-gelijkzijdig viervlak

Definitie
Een half-gelijkzijdig viervlak is een viervlak waarvan precies twee zijvlakken gelijke oppervlakte hebben.
De gemeenschappelijke ribbe van die twee vlakken heet de topribbe van het viervlak.

Stelling 1
(1) In een half-gelijkzijdig viervlak is er een vlak dat zowel zwaartevlak als bissectricevlak is.
(2) Dat vlak bevat ook het kortste verbindingslijnstuk tussen de topribbe en de overstaande ribbe (van die topribbe).

Bewijs:

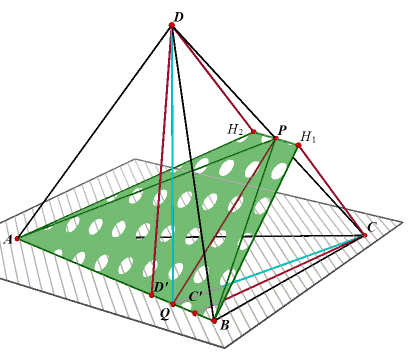In het viervlak ABCD hebben de driehoeken ABC en ABD gelijke oppervlakte. De topribbe van het viervlak is dus de ribbe AB.
Zij P het midden van de ribbe CD.
We zullen aantonen dat het vlak ABP zwaartevlak en bissectricevlak is van het viervlak.

(1) Omdat P het midden is van CD is het vlak ABP een zwaartevlak van ABCD.
H₁ en H₂ zijn opvolgend de projecties van C en D op het vlak ABP.
In het vlak door CH₁ en DH₂ liggen de driehoeken PCH₁ en PDH₂ die congruent zijn (ZHZ), zodat:
CH₁ = DH₂
De viervlakken C.PAB en D.PAB hebben gelijke inhoud (gelijke hoogte en gemeenschappelijk grondvlak).
Bekijken we dezelfde viervlakken, maar nu als P.ABC en P.ABD dan zijn de bijbehorende afstanden van P tot ABC en tot ABD eveneens gelijk, immers Opp(ABC) = Opp(ABD).
P heeft dus gelijke afstanden tot de vlakken ABC en ABD.
P ligt dus in het bissectricevlak van die vlakken.
ABP is dus eveneens bissectricevlak van ABCD.

(2) De projectie van C op AB is C', die van P op AB is Q en die van D op AB is D'.
Nu is CC' = DD' (vanwege de gelijke oppervlakte van ABC en ABD).
Door projectie van CP en DP op AB is ook QC' = QD'.
De rechthoekige driehoeken CC'Q en DD'Q zijn dan congruent (ZHZ), waaruit volgt dat QC = QD.
Driehoek QCD is dan een gelijkbenige driehoek met tophoek C. P is het midden van de basis. Dus QP _|_ CD.
We wisten reeds (door de projectie), dat PQ _|_ AB.
Het lijnstuk PQ is dus het gemeenschappelijk loodlijnstuk van de lijnen AB en CD, en dat lijnstuk ligt in vlak ABP. ¨

Gevolg 1
Hebben de beide andere zijvlakken, CDA en CDB, eveneens gelijke oppervlakte, dan is Q dus het midden van AB.
Het lijnstuk PQ is dan zowel bimediaan (verbindingslijnstuk van de middens van overstaande ribben) als loodrecht verbindingslijnstuk van AB en CD.
[einde Opmerking]

Gelijkzijdig viervlak
We bewijzen allereerst een hulpstelling (die we gebruiken in stelling 2).

Hulpstelling
De meetkundige plaats van de middens van de verbindingslijnstukken van twee kruisende lijnen is het middelloodvlak van het loodrechte verbindingslijnstuk van die kruisende lijnen.

Bewijs:

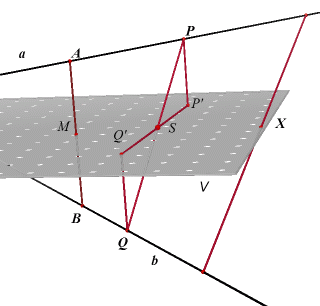De lijnen a en b kruisen elkaar. Het lijnstuk AB, met midden M, is de loodrechte afstand. Het vlak V is het middelloodvlak van AB.

(a) P en Q zijn twee willekeurige punten van opvolgend a en b. P', Q' zijn hun projecties op V.
Nus is PP' = AM en QQ' = BM, zodat PP' = QQ'. Maar ook PP' // QQ', zodat PP'QQ' een parallellogram is. PQ snijdt P'Q' in het punt S, het midden van PQ. Maar S ligt ook in V.

(b) Bij een willekeurig punt X van het vlak V is een lijn te vinden die a en b beide snijdt.
Immers de snijlijn van een vlak door X en a en een vlak door X en b gaat door X en snijdt a en b. ¨

Klik hier >< voor een Cabri 3D applet bij deze hulpstelling.

Definitie
Een gelijkzijdig viervlak is een viervlak waarvan alle zijvlakken gelijke oppervlakte hebben.

Stelling 2
(1) In een gelijkzijdig viervlak vallen de drie bimedianen en de loodrechte verbindingslijnenstukken van overstaande ribben samen.
(2) Van een gelijkzijdig viervlak zijn de overstaande ribben twee aan twee aan elkaar gelijk.

Bewijs:

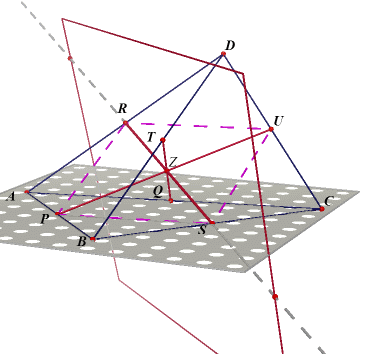(1) Een gelijkzijdig viervlak heeft drie bimedianen: PU, QT, RS, die volgens het Gevolg van stelling 1 samenvallen met de loodrechte verbindingslijnstukken van de overstaande ribben.

(2) De lijnstukken RU en PS zijn beide middenparallellen (opvolgens in driehoek ACD en driehoek ABC) en zijn dus beide evenwijdig met en geljk aan de helft van AC.
PU en RS liggen dan in hetzelfde vlak, en PSUR is dus een parallellogram.
De bimedianen PU en RS snijden elkaar dan en delen elkaar middendoor.
En dat geldt ook voor elk ander tweetal: de bimedianen gaan door hetzelfde punt Z.
Elk tweetal loodrechte verbindingslijnstukken staat loodrecht op elkaar, omdat de een in het middelloodvlak van de ander ligt (zie Hulpstelling).
PSUR is dus een ruit, waaruit weer volgt dat AC = BD.
Analoog geldt dat voor de andere overstaande ribben. ¨

Klik hier >< voor een Cabri 3D applet bij stelling 2 (opent in een NieuwVenster; automatisch draaiend).

Gevolg 2
Het snijpunt Z van de bimedianen ligt in elk van de zwaartevlakken. Z is dus zwaartepunt van het viervlak.
Het punt Z ligt ook in alle bissectricevlakken. Het punt Z is dus middelpunt van de inbol van het viervlak.
Z ligt ook in elk van de middelloodvlakken van de ribben. Z is dus eveneens middelpunt van de ombol van het viervlak.
[einde Gevolg]

[p : hgelijkzviervlak.htm] laatste wijziging op: 26-09-2005