Inhoud van een bol en van een bolsegment

Overzicht  ][  Oppervlakte bol  |  Overzicht stereo  |  Cabri 3D

Overzicht terug

  1. Inhoud van een bol
  2. Inhoud van een bolsegment
¤. Zie ook de pagina "De bol".
¤ Zie evt. ook het artikel "Inhoud en oppervlakte van een bol zonder integraalrekening"
(Dick Klingens, sep. 2008, ongepubliceerd / PDF-bestand, ca. 800 Kb)

Nb. Zie voor de naamgeving en bijbehorende definities de pagina "Oppervlakte van een bol ...".

1. Inhoud van een bol terug

figuur 1
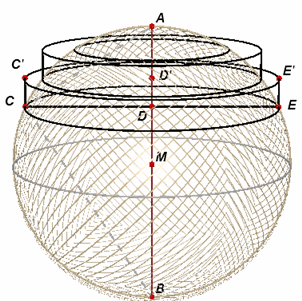
inhbol1 Om de inhoud van een bol (middelpunt M) met straal R te berekenen, verdelen we een middellijn AB in n gelijke stukken. Elk stuk heeft de lengte Dx (zoals in de figuur DD' = EE').
Door de deelpunten (D, D', ...) brengen we vlakken aan, loodrecht op AB, die de bol volgens cirkels snijden.

Als D het p-de deelpunt is (gerekend vanaf het punt A), stellen we de lengte van AD gelijk aan xp.
Zodat: xp = p · Dx.
Met elk van de snijcirkels als grondvlak en Dx als hoogte beschrijven we een cilinder (zoals CEE'C').

De inhoud van de bol is dan de limiet van de som van de inhouden alle cilinders, als n nadert tot oneindig (daarmee nadert Dx tot 0).

We berekenen nu de inhoud I' van de cilinder waarvan het grondvlak door D gaat (daarbij is dus AD = xp):
I' = p · (CD)2 · EE' = p · AD · DB · Dx = p · xp · (2R - xp) · Dx
immers in de rechthoekige driehoek ACB is CD2 = AD · DB.

Voor de inhoud I van de bol vinden we dan:

inhbol(form1)

Zodat:

Stelling 1
De inhoud van een bol met straal R is gelijk aan 4/3pR3.

2. Inhoud van een bolsegment terug

Op dezelfde manier vinden we de inhoud I van het bolsegment dat bepaald wordt door het vlak door D loodrecht op AB (zie figuur 1), waarbij AD = h (de hoogte van het segment).
We vinden hiervoor:

inhbol(form2)

Waarmee is aangetoond dat:

Stelling 2
De inhoud van een bolsegment met hoogte h is gelijk aan 1/3ph2(3R - h), waarbij R de straal van de bol is.

begin pagian
[p: inhoudbol.htm] laatste wijziging op: 20-09-2008 (17-09-08)