Vierzijdig prisma en bol
Overzicht ][ Overzicht stereo | Axioma's | Cabri 3D
Gegeven: Het vierzijdige lichaam ABCD.EFGH heeft een omgeschreven bol (zie figuur 1).
De opstaande zijvlakken ABFE, BCGF, ... zijn dan koordenvierhoeken.
| figuur 1 | figuur 2 | |
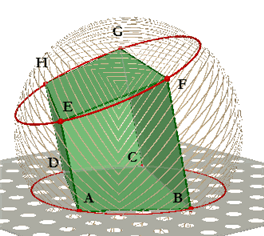 |
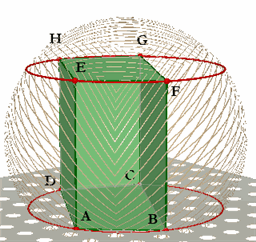 |
Gevolg. Als ABCD.EFGH een prisma is, dan is het een recht
prisma. Immers, de opstaande zijvlakken (zoals ABFE) van een prisma zijn parallellogrammen, en daarmee dus rechthoeken (de punten A, B, E, F liggen op een cirtkel). Dan is: EA _|_ AB en EA _|_ AD, zodat EA _|_ ABCD. Het prisma moet dus recht zijn (zie figuur 2). |
We hebben dus bewezen:
| Stelling 1 Als om een vierzijdig prisma een bol beschreven kan worden, is het prisma recht (en zijn grondvlak en bovenvlak koorenvierhoeken). |
De omgekeerde stelling geldt eveneens:
| Stelling 2 Als het grondvlak van een recht prisma een koordenvierhoek is, dan heeft het prisma een omgeschreven bol. |
Bewijs:
We brengen een bol aan door de punten A, B, D en E (zie weer figuur 2).
Omdat het grondvlak ABCD een koordenvierhoek is, gaat de omcirkel van driehoek ABD ook
door het punt C.
De bol gaat dus ook door C.
Daar ABFE een koordenvierhoek is (het is een rechthoek), gaat de omcirkel van driehoek ABE
ook door het punt F.
De bol gaat dus ook door F.
Op dezelfde manier tonen we aan dat de bol ook door G en H gaat.¨
Definitie: Een bol die aan alle begrenzende vlakken van een prisma raakt, heet de ingeschreven bol van het prisma.
Voor een prisma met een ingeschreven bol geldt:
| Stelling 3 Als een vierzijdig prisma een ingeschreven bol heeft, dan is (1) een loodrechte doorsnede van het prisma een raaklijnenvierhoek, en is (2) de hoogte van het prisma gelijk aan de middellijn van de ingeschreven cirkel van die loodrechte doorsnede. |
Bewijs:
| figuur 3 | |
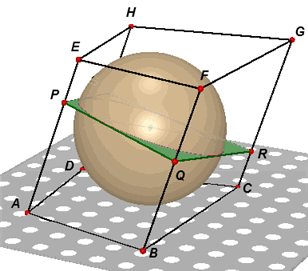 |
Zie figuur 3. (1) Twee paar evenwijdige zijvlakken raken aan de ingeschreven bol. De raakpunten van die vlakken zijn dus de eindpunten van een middellijn van een grote cirkel van de ingeschreven bol. Het vlak waarin de cirkel door de raakpunten met die vlakken ligt, staat loodrecht op die zijvlakken en is dus een loodrechte doorsnede. De vierzijden van de doorsnede zijn daarmee raaklijnen aan de grote cirkel, en is dus een raaklijnenvierhoek. (2) De afstand tussen het grondvlak en het bovenvlak (ook evenwijdige vlakken) is eveneens gelijk aan de middellijn van de bol, immers die vlakken zijn ook raakvlak.¨ |
![]()
[p: prismabol.htm] laatste wijziging op: 16-09-2008 (150908)