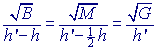Prismoïde, obelisk, anti-prisma

Definities | Inhoud prismoïde ][ Prisma | Inhoud | Overzicht stereo | Cabri 3D

1. Definities prismoïde, obelisk, anti-prisma

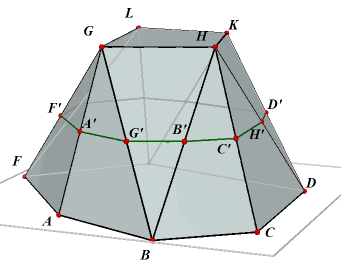
Definities
(Zie figuur 1a) Een convex veelvlak waarvan de hoekpunten in twee evenwijdige vlakken liggen, heet prismoïde (ook wel prismatoïde; Eng. prismatoid, prismoid)
De zijvlakken in de evenwijdige vlakken noemt men grond- en bovenvlak; de andere zijvlakken heten opstaande zijvlakken
De afstand tussen de evenwijdige vlakken heet de hoogte van de prismoïde.

figuur 1a		figuur 1b

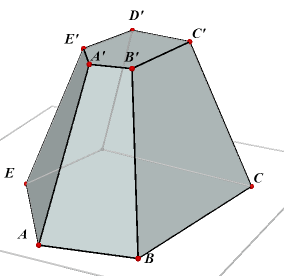
In deze prismoïde is het zogenoemde middenvlak A'G'B'... aangebracht. Dit is het vlak door de middens van de opstaande ribben.		Deze figuur toont een obelisk (zijvlakken zijn trapezia).
Klik hier >< voor een Cabri 3D applet van een prismoïde (in een NieuwVenster, automatisch draaiend).		Klik hier >< voor een Cabri 3D applet van een obelisk (in een NieuwVenster, automatisch draaiend).

Definitie
(Zie figuur 1b) Een prismoïde waarvan alle opstaande zijvlakken trapezia (of parallellogrammen) zijn, heet obelisk.

En volvolgens nog een tweede bijzondere prismoïde.

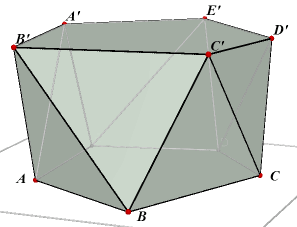
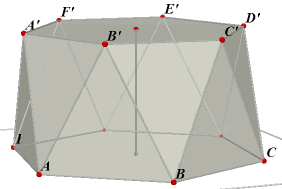
Definitie
(Zie figuur 1c) Een anti-prisma is een prismoïde waarvan alle opstaande zijvlakken driehoeken zijn.
Zijn grond- en bovenvlak van een anti-prisma regelmatige veelhoeken en ligt het middelpunt van het bovenvlak recht boven het middelpunt van het grondvlak, dan spreken we van een regelmatig anti-prisma (zie figuur 1e).

Wanneer wordt uitgegaan van een 'gewoon' prisma, waarbij dan het bovenvlak "iets" gedraaid wordt tov. het ondervlak dan krijgen we (uiteraard) ook een anti-prisma (zie figuur 1d). In de literatuur wordt deze vorm vaak (en onterecht) als definitie gegeven voor een anti-prisma.

figuur 1c		figuur 1d		figuur 1e

Klik hier >< voor een Cabri 3D applet van figuur 1c (in een NieuwVenster; automatisch draaiend).
Klik hier >< voor een Cabri 3D applet van figuur 1d (in een NieuwVenster; automatisch draaiend).
Klik hier >< voor een Cabri 3D applet van figuur 1e (in een NieuwVenster; automatisch draaiend).

2. Inhoud prismoïde

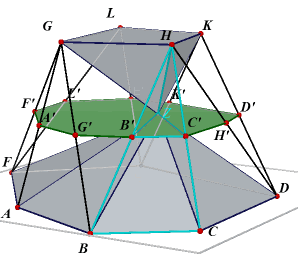We kiezen in het middenvlak, het vlak dat gaat door de middens van de opstaande ribben, een willekeurig punt Z.
Er ontstaan dan in ieder geval twee piramides: Z.ABCDEF en Z.GHKL.

Zijn nu G, B en M opvolgend de oppervlaktes van het grondvlak, het bovenvlak en het middenvlak.
De inhouden van die piramides zijn opvolgend I_G = ¹/₆Gh en I_B = ¹/₆Bh, waarbij h de hoogte is van de prismoïde.

De rest van de prismoïde bestaat uit drie of vierzijdige piramides met top Z en met als grondvlak een van de opstaande zijvlakken van de prismoïde.
We bekijken nu Z.BCH.
Omdat Opp(BCH) = 4.Opp(B'C'H), geldt ook
Inh(Z.BCH) = 4 . Inh(Z.B'C'H)

Maar Inh(Z.B'C'H) = Inh(H.ZB'C'), en dit laatste viervlak heeft ¹/₂h als hoogte, zodat
Inh(Z.BCH) = 4 . ¹/₃ Opp(ZB'C') . ¹/₂h
Sommatie over alle deeldriehoeken ZB'C', ZC'H', ... van het middenvlak geeft dan voor de inhoud I_Z van de resterende piramides: I_Z = ⁴/₆ Mh.
De inhoud van de prismoïde is dan

I = I_G + I_B + I_Z = ¹/₆ h (G + B + 4M)

Nb. Bovenstaande inhoudsformule geldt dus eveneens voor de obelisk en anti-prisma.

Gevolg
Omdat het prisma, de piramide en de afgeknotte piramide bijzondere prismoïden zijn (bij het prisma is B = G = M; bij de piramide is B = 0 en M = ¹/₄G), zullen de inhoudsformules van die lichamen uit die voor de prismoïde moeten volgen:
prisma: I = ¹/₆ h (G + G + 4G) = Gh
piramide: I = ¹/₆ h (G + 0 + G) = 1/3Gh

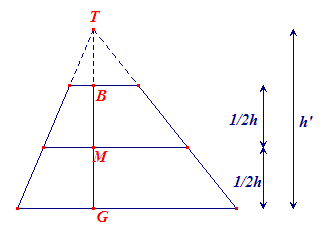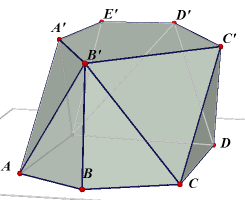
Bij de afgeknotte piramide moeten we eerst nog een uitdrukking vinden voor M.

Hiernaast is een 'as'-doorsnede getekend van een afgeknotte piramide. T is de top van de niet-afgeknotte piramide (met hoogte h').
De punten B, M, G liggen opvolgend in het bovenvlak, middenvlak en grondvlak.
Nu geldt:

waaruit volgt:

Dus:
afgeknotte piramide: I = ¹/₆ h (B + G + B+ G + 2Ö(BG) ) = ¹/₃h (B + G + Ö(BG) )

Zie ook de pagina "Inhoud van viervlak en piramide (en meer)".

[p : prismoide.htm] laatste wijziging op: 14-09-2005